If for an ideal gas, the ratio of pressure and volume is constant and is equal to 1atmL−1, the molar heat capacity at constant pressure would beSolution in Malayalam
(3/2) R
2R
(5/2)R
zero
The correct Answer is:B
By idfinition, H=U+pV, Hence Cp.m=(∂H∂T)P+P(∂V∂T)P
For the given ideal gas, we will have pV=RT⇒{(1atmL−1)V}V=RTorV2=RT(1atmL−1)
Hence 2V(∂V∂T)P=RT(1atmL−1)or(∂V∂T)P=RT2V(1atmL−1)
Also U=32RT⇒(∂U∂T)P=32R
With these, Cp.m=32R+p{R2V(1atmL−1)}=32R+R2=2R
Topper's Solved these Questions
- BOOK - BRILLIANT PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - LEVEL-II (Assertion-Reason Type)18videos
CHEMICAL THERMODYNAMICS
- BOOK - BRILLIANT PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - LEVEL-III52videos
CHEMICAL THERMODYNAMICS
- BOOK - BRILLIANT PUBLICATIONCHAPTER - CHEMICAL THERMODYNAMICS EXERCISE - LEVEL-I92videos
CHEMICAL THERMODYNAMICS
- BOOK - BRILLIANT PUBLICATIONCHAPTER - CHEMICAL BONDING AND MOLECULAR STRUCTUREEXERCISE - QUESTION (LEVEL -ll)42videos
CHEMICAL BONDING AND MOLECULAR STRUCTURE
- BOOK - BRILLIANT PUBLICATIONCHAPTER - CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIESEXERCISE - QUESTIONS (LEVEL-III ( Linked Comprehension Type ))12videos
CLASSIFICATION OF ELEMENTS AND PERIODICITY IN PROPERTIES
Similar Questions
Assertion : Heat of neutralisation of HNO3, and NaOH is almost same as that of HCl and KOH.
Reason : Both HNO3, and HCl are strong acids and NaOH and KOH are strong bases. : if both (A) and (R) are correct and (R) is the correct explanation of(A)., If both (A) and (R) are correct, but (R) is not the correct explanation of(A)., If(A) is correct, but (R) is incorrect., If both (A) and (R) are incorrect.02:05View Solution1.0 mole of a monoatomic ideal gas is expanded from state (1) to state (2) as shown in the figure. Calculate ti work done for the expansion of gas from state (1) to state (2) at 298 K
 01:20View Solution
01:20View SolutionIn ....... process, work is done at the expense of internal energy.
01:42View SolutionWhich of the following species are hypervalent ?
(l) ClO−4
(ll) BF3
(lll) SO2−4
(lV) CO2−305:33View SolutionThe heats of formation (ΔH∘f) of the oxides of the third period, sodium to chlorine, are in kJ mol−1
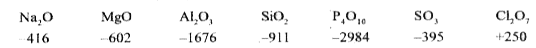
Based on these data, answer the following questions
Which oxide has maximum negative heat of formation per oxygen atom?02:05View SolutionThe molar specific heat at constant pressure of an ideal gas is (7/2R). The ratio of specific heat at constant pressure to that at constant volume is
01:41View SolutionThe ratio of the molar heat capacities of a diatomic gas at constant pressure to that at constant volume is
06:57View SolutionFor n moles of a gas, the difference between the molar heat capacity at constant pressure and that at constant volume is equal to "…............." .
01:31View SolutionShow that for an ideal gas the difference between the molar heat capacities at constant pressure and at constant volume is equal to the universal gas constant (R).
01:50View SolutionThe molar specific heat at constant pressure of an ideal gas is (7/2R). The ratio of specific heat at constant pressure to that at constant volume is
01:15View SolutionThe molar specific heat at constant pressure of an ideal gas is (7//2)R . The ratio specific heats at constant pressure to that at constant volume is ………. .
04:40View SolutionObtain the relation between specific heat capacity at constant pressure and specific heat capacity at constant volume for an ideal gas.
01:30View SolutionThe molar specific heat at constant pressure of an ideal gas is 72R. The ratio of specific heat at constant pressure to that at constant volume is ……….
01:47View SolutionThe ratio of the molar heat capacities of a diatomic gas at constant pressure to that at constant volume is
01:39View SolutionThe molar specific heat at constant pressure of an ideal gas is (7//2 R) . The ratio of specific heat at constant pressure to that at constant volume is
01:25View Solution

