1 kg द्रव्यमान का कोई पिण्ड किसी कालाश्रित बल →F=(2tˆi+3t2ˆj)N यहाँ ˆiऔर ˆj x और y अक्ष के अनुदिश मात्रक सदिश है के अधीन गति आरम्भ करता है तो समय t पर इस बल द्वारा विकसित शक्ति क्या होगी
(2t2+4t4) वाट
(2t3+3t4) वाट
(2t3+3t5) वाट
(2t+3t3) वाट
The correct Answer is:C
प्रश्नानुसार,
1 किलोग्राम द्रव्यमान वाले पिण्ड जो कि कलाश्रित बल की क्रिया में गति कर रहा है।
F=(2tˆi+3t2ˆj)N
जहाँ, ˆi तथा ˆj, x तथा y- अक्ष के सापेक्ष इकाई हैं।
F=ma
⇒a=Fm
⇒a=(2tˆi+3t2ˆj)1 {∵m=1 kg}
a=(2tˆi+3t2ˆj)मी/से2
∵ त्वरण, a=dvdt
dv=adt
दोनों ओर समाकलन करने पर, हम पाते हैं कि,
∫dv=∫adt=∫(2tˆi+3t2ˆj)dt
v=t2ˆi+t3ˆj
∵ t समय में बल द्वारा उत्पन्न शक्ति,
P=F⋅v=(2tˆi+3t2ˆj)⋅(t2ˆi+t3ˆj)
=(2t⋅t2+3t2t3)
P=(2t3+3t5) वाट
Topper's Solved these Questions
Similar Questions
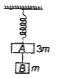
दो गुटकों A और B के द्रव्यमान, क्रमश: 3m तथा m हैं। ये आपस में एक द्रव्यमानहीन, अवितान्य डोरी से जुड़े हैं। इस पूरे निकाय को, आरेख में दर्शाए गए अनुसार एक द्रव्यमानरहित स्प्रिंग (कमानी) द्वारा लटकाया गया है। डोरी को काट देने के तुरन्त पश्चात् A और B के त्वरण के परिमाण होंगे क्रमशः
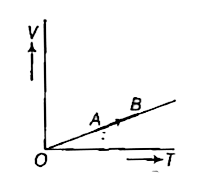
View Solutionकिसी एकपरमाणुक गैस के आयतन (V) में ताप (T) के साथ विचरण ग्राफ में दर्शाए अनुसार होता है। अवस्था A से अवस्था B तक जाने की प्रक्रिया में गैस द्वारा किए गए कार्य और इसके द्वारा अवशोषित ऊष्मा का अनुपात है
View SolutionConsider a line vec r=hat i+t(hat i+hat j+hat k) and a plane (vec r-(hat i+hat j))*(hat i-hat j-hat k)=1
View SolutionFind the shortest distance between the given line
→r=(3−t)ˆi+(4+2t)ˆj+(t−2)ˆk
→r=(1+s)ˆi+(3s−7)ˆj+(2s−2)ˆk
View Solutionउस समतल का सदिश समीकरण ज्ञात कीजिये जो बिन्दुओ ˆi−ˆk और 3ˆi+2ˆj+2ˆk से होकर गुजरता है तथा सदिश ˆi−2ˆj+3ˆk के समांतर है
View Solutionयदि →a=ˆi+ˆj+ˆk,→b=2ˆi−ˆj+3ˆk और →c=ˆi−2ˆj+ˆk तो निम्नलिखित ज्ञात करे
→p जो →a और →b दोनों पर लंब है एवं →p.→c=15
View Solutionयदि →a=ˆi+ˆj+ˆk,→b=2ˆi−ˆj+3ˆk और →c=ˆi−2ˆj+ˆk तो सदिश 2→a−→b+3→c के समांतर एक मात्रक सदिश ज्ञात कीजिए ।
View Solutionसदिश →a=2ˆi+3ˆj−ˆk और →b=ˆi−2ˆj+ˆk के परिणामी के समान्तर एक ऐसा सदिश ज्ञात कीजिए जिसका परिमाण 5 इकाई है।
View Solutionयदि →a=ˆi+2ˆj−3ˆk तथा →b=3ˆi−2ˆj+ˆk हो , तो सिद्ध कीजिए कि (→a+→b) और (→a−→b) परस्पर लम्ब है। (2→a+→b) और (→a+2→b) के बीच का कोण ज्ञात कीजिए।
View Solutionसदिश →a+→b और →a−→b कि लम्ब दिशा में मात्रक सदिश ज्ञात कीजिए जहाँ →a=3ˆi+2ˆj+2ˆk और →b=ˆi+2ˆj−2ˆk है।
View Solutionएक बल 2ˆi+ˆj+ˆk एक बिन्दु A जिसका स्थिति सदिश2ˆi−ˆj है , पर कार्य करता है। बल का मूलबिंदु के सापेक्ष आघूर्ण ……. होगा।
View Solutionसदिश ˆi…………. अक्ष के समांतर एकांक सदिश है।
View Solutionबिन्दु (1,2,3) से जाने वाली तथा समतलो →r.(ˆi−ˆj+2ˆk)=5 और →r.(3ˆi+ˆj+ˆk)=6 के समान्तररेखा के सदिश समीकरण ज्ञात कीजिए।
View Solutionरेखाएं जिनकी सदिश समीकरण निम्नलिखित हैं , के बीच की न्यूनतम दूरी ज्ञात कीजिए-
→r=(1−t)ˆi+(t−2)ˆj+(3−2t)ˆk और →r=(s+1)ˆi+(2s−1)ˆj−(2s+1)ˆk
View Solutionसमतल का सदिश समीकरण जो बिन्दु ˆi−2ˆj+ˆk से होकर जाता है तथा सदिश 3ˆi−ˆj,2ˆk−ˆiसमान्तरहै -
View Solutionसमतलो →r.(ˆi−ˆj+ˆk)+3=0 तथा →r.(ˆi+2ˆj+k)−5=0के बीच का कोण है -
View Solution
