If V1:V2 = 1:2 and V1+V2=147, then what is the value of V2-V1.
यदि V1:V2 = 1:2 तथा V1+V2=147 है, तो V2-V1 का मान क्या होगा ?
48
56
98
49
To solve the problem, we need to find the values of V1 and V2 based on the given ratio and their sum. Here’s the step-by-step solution:
Step 1: Understand the ratio
We are given that V1:V2 = 1:2. This means that for every 1 part of V1, there are 2 parts of V2.
Step 2: Express V1 and V2 in terms of a variable
Let’s denote V1 as x. According to the ratio, V2 will then be 2x.
Step 3: Set up the equation using the sum
We know that V1 + V2 = 147. Substituting the expressions for V1 and V2, we get:
x+2x=147
Step 4: Simplify the equation
Combine like terms:
3x=147
Step 5: Solve for x
To find the value of x, divide both sides by 3:
x=1473=49
Step 6: Find the values of V1 and V2
Now that we have x, we can find V1 and V2:
- V1 = x = 49
- V2 = 2x = 2 * 49 = 98
Step 7: Calculate V2 - V1
Now we need to find V2 - V1:
V2−V1=98−49=49
Final Answer
Thus, the value of V2 - V1 is 49.
---
We are given that V1:V2 = 1:2. This means that for every 1 part of V1, there are 2 parts of V2.
Let’s denote V1 as x. According to the ratio, V2 will then be 2x.
We know that V1 + V2 = 147. Substituting the expressions for V1 and V2, we get:
x+2x=147
Combine like terms:
3x=147
To find the value of x, divide both sides by 3:
x=1473=49
Now that we have x, we can find V1 and V2:
- V1 = x = 49
- V2 = 2x = 2 * 49 = 98
Now we need to find V2 - V1:
V2−V1=98−49=49
Thus, the value of V2 - V1 is 49.
Topper's Solved these Questions
Similar Questions
Knowledge Check
If modulation index μ=12 and V2=2 then VC=?
A4B2C6D8If a2+1a2=7andV1andV2 are the minimum and the maximum values of a3+1a3,then V2−V1 is equal to ?
A−36B36C72D−18In the circuit, the battery is ideal. A voltmeter of inifinite resistance is connected in turn across R1 and R2, giving reading of V1 and V2 respectively.
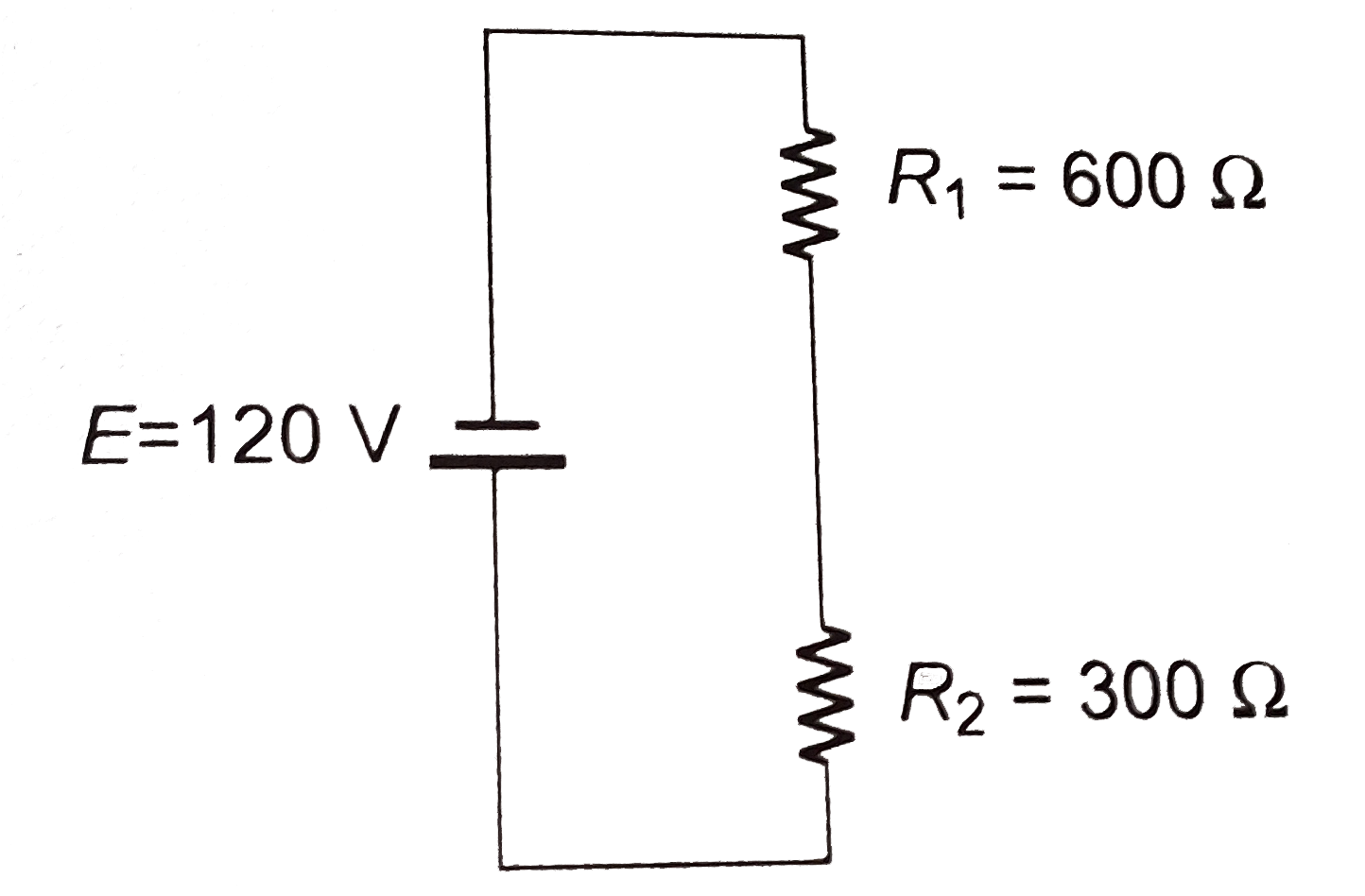 .
.
(i) V1=80V
(ii) V1=60V
(iii) V2=30V
(iv) V2=40V.A(i),(ii)B(ii),(iii)C(iii),(iv)D(i),(iv)
A regular triangular pyramid is cut by 2 planes which are parallel to its base. The planes trisects the altitude of the pyramid. Volume of top, middle and bottom part is V1,V_2andV_3respectively.WˆisthevalueofV_1: V_2: V_3?
एक सम त्रिभुजाकार पिरामिड को दो तल जो उसके आधार के समांतर है, द्वारा काया जाता है। तल पिरामिड की ऊँचाई को समत्रिभाजित करते है उसके ऊपरी, मध्य तथा निचले भाग का आयतन क्रमशः V_1, V2तथाV_3है।V_1: V_2: V_3 का मान क्या है?
View SolutionIf f(x)=log{u(x)v(x)}, u(1)=v(1) and u′(1)=v′(1)=2 , then find the value of f′(1) .
View SolutionEvaluate : 13 ∫1+2vv2+v+1dv
View SolutionTwo batteries V1 and V2 are connected to three resistors as shown below. If V1=2Vand V2 = 0 V, the current I = 3 mA. If V1 = 0 V and V2 = 4V, the current I = 4mA. Now, if V1 = 10 V and V2 = 10 V, the current I will be-

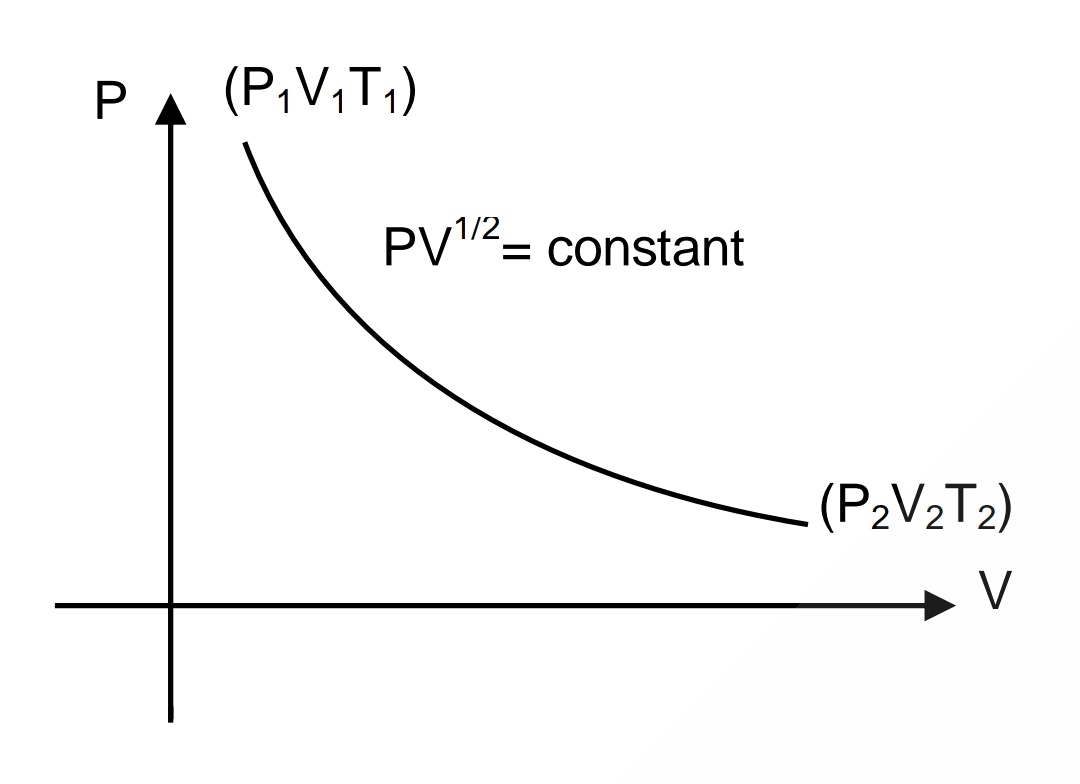
View SolutionA gas follows PV12=constant as shown. If V2=2V1 , find T2T1
View Solution
