The area of a field in the shape of a triangle with each side x metre is equal to the area of another triangular field having sides 50m , 70m and 80m. The value of x is closest to :
प्रत्येक भुजा x मीटर वाले एक त्रिभुज का क्षेत्रफल एवं विमाओं 50m , 70m और 80m वाले त्रिभुज का क्षेत्रफल समान है,x का मान ज्ञात कीजिये ?
65.5
63.2
62.5
61.8
To solve the problem, we need to find the value of x such that the area of an equilateral triangle with side length x meters is equal to the area of another triangle with sides 50 m, 70 m, and 80 m.
1. Calculate the area of the triangle with sides 50 m, 70 m, and 80 m using Heron's formula.
- First, calculate the semi-perimeter s:
s=50+70+802=100 m
2. Apply Heron's formula to find the area A:
- Heron's formula states:
A=√s(s−a)(s−b)(s−c)
- Where a=50, b=70, and c=80:
A=√100(100−50)(100−70)(100−80)
A=√100×50×30×20
3. Calculate the values inside the square root:
- First, calculate 100×50=5000
- Then, 5000×30=150000
- Finally, 150000×20=3000000
- Thus, we have:
A=√3000000
4. Simplify the area calculation:
- We can simplify √3000000:
A=√3×1000000=1000√3 m2
5. Calculate the area of the equilateral triangle with side x:
- The area A of an equilateral triangle is given by:
A=√34x2
6. Set the areas equal to each other:
- We have:
1000√3=√34x2
7. Eliminate √3 from both sides:
- Dividing both sides by √3:
1000=14x2
8. Solve for x2:
- Multiply both sides by 4:
4000=x2
9. Take the square root to find x:
- Thus,
x=√4000=63.2455532 m
10. Round to the nearest decimal:
- The value of x is closest to:
x≈63.2 m
Final Answer:
The value of x is closest to 63.2 m.
- First, calculate the semi-perimeter s:
s=50+70+802=100 m
- Heron's formula states:
A=√s(s−a)(s−b)(s−c)
- Where a=50, b=70, and c=80:
A=√100(100−50)(100−70)(100−80)
A=√100×50×30×20
- First, calculate 100×50=5000
- Then, 5000×30=150000
- Finally, 150000×20=3000000
- Thus, we have:
A=√3000000
- We can simplify √3000000:
A=√3×1000000=1000√3 m2
- The area A of an equilateral triangle is given by:
A=√34x2
- We have:
1000√3=√34x2
- Dividing both sides by √3:
1000=14x2
- Multiply both sides by 4:
4000=x2
- Thus,
x=√4000=63.2455532 m
- The value of x is closest to:
x≈63.2 m
The value of x is closest to 63.2 m.
Topper's Solved these Questions
Similar Questions
Knowledge Check
The area of a equilateral triangular park is equal to 5√3times the area of a triangular field with sides 18 m, 80 m and 82 m. What is the side of the triangular park?
A125 mB120 mC140 mD100 m
What is the area of a triangle with sides 35 cm, 84 cm and 91 cm ?
35 cm, 84 cm तथा 91 cm भुजाओं वाले किसी त्रिभुज का क्षेत्रफल कितना है?
View SolutionThe area of a circular park is approximately equal to the seven-fifteenth of the area of a triangular park with sides 110 m, 600 m, and 610 m. Find the diameter of the park.
एक वृत्ताकार पार्क का क्षेत्रफल एक ऐसे त्रिभुजाकार मैदान जिसकी भुजाएं 110 m, 600 m और 610 m हैं, के क्षेत्रफल के 7/15 (seven-fifteenth) के लगभग बराबर है | पार्क का व्यास कितना है?
View SolutionA triangle has sides 25, 39 and 34 units. If the area of a square exceeds the area of this triangle by 21 units, then the side of the square is:
एक त्रिभुज की भुजाएँ 25, 39 और 34 इकाई हैं। यदि एक वर्ग का क्षेत्रफल इस त्रिभुज के क्षेत्रफल से 21 इकाई अधिक है तो वर्ग की भुजा ज्ञात कीजिए।
View SolutionPA and PB are tangents to the circle and O is the centre of the circle. The radius is 5 cm and PO is 13 cm. If the area of the triangle PAB is M, then the value of √M15 is :
PA और PB वृत्त के स्पर्शरेखा है और O वृत्त का केंद्र है। त्रिज्या 5 सेमी और PO =13 सेमी है। यदि त्रिभुज PAB का क्षेत्रफल M है, तो √M15 का मान है: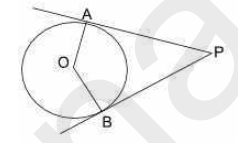
View SolutionThe sides of a triangular park are 200 m, 210 m and 290 m. The area of the park (in hectares) is:
किसी त्रिभुजाकार उद्यान की भुजाएँ 200 मी, 210 मी और 290 मी की हैं | इस उद्यान का क्षेत्रफल ( हेक्टेयर में ) है:
View SolutionThe in-radius of a triangle is 6 cm, and the sum of the length of its sides is 50cm. The area of the triangle (in sq. cm) is
एक त्रिभुज को अंतः त्रिज्या 6 सेमी है, तथा इसके भुजाओं के लंबाई का योग 50 सेमी है। त्रिभुज का क्षेत्रफल (वर्ग सेमी में) ज्ञात करें।
View SolutionTwelve sticks, each of length one unit, are used to form an right-angled triangle. The area of the triangle is :
बारह छड़ियाँ, जिनमें से प्रत्येक की लंबाई एक इकाई है, का इस्तेमाल एक समकोण त्रिभुज बनाने के लिए किया जाता है | इस त्रिभुज का क्षेत्रफल ज्ञात करें |
View Solution
