What is the area of the largest square which can be inscribed in a circle of radius 14 cm? (π=227)
उस सबसे बड़े वर्ग का क्षेत्रफल ज्ञात करें जिसे 14 सेमी त्रिज्या वाले वृत्त के भीतर खींचा जा सकता है |
392cm2
484cm2
196cm2
784cm2
To find the area of the largest square that can be inscribed in a circle of radius 14 cm, we can follow these steps:
Step 1: Understand the relationship between the square and the circle
The diagonal of the inscribed square is equal to the diameter of the circle.
Step 2: Calculate the diameter of the circle
The diameter D of the circle can be calculated using the formula:
D=2×radius
Given the radius is 14 cm:
D=2×14=28 cm
Step 3: Relate the side of the square to its diagonal
Let the side length of the square be a. The diagonal d of the square can be expressed in terms of its side length using the formula:
d=a√2
Since the diagonal of the square is equal to the diameter of the circle, we have:
a√2=28
Step 4: Solve for the side length a
To find a, rearrange the equation:
a=28√2
To simplify 28√2, multiply the numerator and denominator by √2:
a=28√22=14√2 cm
Step 5: Calculate the area of the square
The area A of the square is given by:
A=a2
Substituting a=14√2:
A=(14√2)2=142×(√2)2=196×2=392 cm2
Final Answer
The area of the largest square that can be inscribed in the circle is:
392 cm2
---
The diagonal of the inscribed square is equal to the diameter of the circle.
The diameter D of the circle can be calculated using the formula:
D=2×radius
Given the radius is 14 cm:
D=2×14=28 cm
Let the side length of the square be a. The diagonal d of the square can be expressed in terms of its side length using the formula:
d=a√2
Since the diagonal of the square is equal to the diameter of the circle, we have:
a√2=28
To find a, rearrange the equation:
a=28√2
To simplify 28√2, multiply the numerator and denominator by √2:
a=28√22=14√2 cm
The area A of the square is given by:
A=a2
Substituting a=14√2:
A=(14√2)2=142×(√2)2=196×2=392 cm2
The area of the largest square that can be inscribed in the circle is:
392 cm2
Topper's Solved these Questions
Similar Questions
What is the area of the largest square which can be inscribed in a circle of radius 28 cm?
उस सबसे बड़े वर्ग का क्षेत्रफल ज्ञात करें जिसे 28 सेमी त्रिज्या वाले वृत्त के भीतर खींचा जा सकता है |
View SolutionWhat is the area of the largest circle that can be inscribed in a square of side 28 cm? (Take π=227)
उस सबसे बड़े वृत्त का क्षेत्रफल ज्ञात करें जिसे 28 सेमी भुजा वाले एक वर्ग के भीतर खींचा जा सकता है |
View Solution
Knowledge Check
What is the area of a sector of a circle of radius 14 cm and the central angle 45∘? (Take Π=227)
एक वृत्त के खंड का क्षेत्रफल ज्ञात कीजिए जिसकी त्रिज्या 14 सेमी तथा केंद्रीय कोण 45∘ है | (Π=227)A67cm2B11cm2C70cm2D77cm2
The area of the largest triangle that can be inscribed in a semicircle of radius 4 cm in square centimeters is
सबसे बड़ा त्रिभुज का क्षेत्रफल ज्ञात कीजिए जिसे 4 सेमी के त्रिज्या वाले अर्धवृत्त में अंकित किया गया है ।
View SolutionWhat is the circumference of the largest circle that can be inscribed in a square of side 14 cm? (Takeπ=227)
उस सबसे बड़े वृत्त की परिधि कितनी होगी जिसे 14 सेमी भुजा वाले वर्ग में समाहित किया जा सकता है ॥
View SolutionFind the area and circumference of a circle if the radius is 14 cm. (Take Π=227)
एक वृत्त का क्षेत्रफल तथा परिधि ज्ञात करें यदि त्रिज्या 14 सेमी है |
View SolutionWhat is the area of a sector of a circle of radius 14 cm and the central angle 45∘? (Take Π=227)
एक वृत्त के खंड का क्षेत्रफल ज्ञात कीजिए जिसकी त्रिज्या 14 सेमी तथा केंद्रीय कोण 45∘ है | (Π=227)
View SolutionWhat is the total surface area of a cone which has a radius of 21 cm and a height of 28 cm? (π=227)
उस शंकु का कुल पृष्ठ क्षेत्रफल ज्ञात करें जिसकी त्रिज्या 21 सेमी और ऊंचाई 28 सेमी है|
View SolutionIn the given figure, the ratio of the area of the largest square to that of the smallest square is:
दी गयी आकृति में, सबसे बड़े वर्ग के क्षेत्रफल और सबसे छोटा वर्ग के क्षेत्रफल का अनुपात है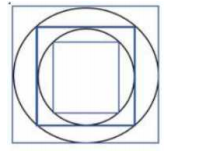
View SolutionWhat are respectively the curved surface area and volume of a hemisphere of radius 21cm? (π=227)
त्रिज्या 21 सेमी वाले अर्धगोले का वक्र पृष्ठ क्षेत्रफल एवं आयतन ( क्रमशः ) ज्ञात करें |
View Solution