The circumference of the base of a cylindrical vessel is 158.4cm and its height is 1 m . How many liters of water can it hold(correct to one decimal place)?
एक बेलनाकार पतीले के आधार की परिधि 158.4 सेमी है और इसकी ऊंचाई 1 मी है। इसके कितने लीटर पानी की क्षमता है (एक दशमलव
स्थान तक ) (Take π=227)
199.6
198.2
200.8
186.4
To solve the problem of finding the capacity of a cylindrical vessel given its circumference and height, we can follow these steps:
Step 1: Find the Radius of the Cylinder
The circumference C of the base of the cylinder is given by the formula:
C=2πr
Given that C=158.4cm and using π=227, we can rearrange the formula to find the radius r:
2πr=158.4
Substituting the value of π:
2×227×r=158.4
Now, simplify:
447r=158.4
To isolate r, multiply both sides by 744:
r=158.4×744
Calculating this gives:
r=25.2cm
Step 2: Convert Height to Centimeters
The height h of the cylinder is given as 1 meter. We need to convert this to centimeters:
h=1m=100cm
Step 3: Calculate the Volume of the Cylinder
The volume V of a cylinder is given by the formula:
V=πr2h
Substituting the values of π, r, and h:
V=227×(25.2)2×100
Calculating (25.2)2:
(25.2)2=635.04
Now substituting this back into the volume formula:
V=227×635.04×100
Calculating 227×635.04:
V=22×90.720=1995.84cm3
Now, since 1cm3=0.001liters:
V=1995.84×0.001=1.99584liters
Step 4: Round to One Decimal Place
Rounding 1.99584 to one decimal place gives:
V≈199.6liters
Thus, the cylindrical vessel can hold approximately 199.6 liters of water.
---
The circumference C of the base of the cylinder is given by the formula:
C=2πr
Given that C=158.4cm and using π=227, we can rearrange the formula to find the radius r:
2πr=158.4
Substituting the value of π:
2×227×r=158.4
Now, simplify:
447r=158.4
To isolate r, multiply both sides by 744:
r=158.4×744
Calculating this gives:
r=25.2cm
The height h of the cylinder is given as 1 meter. We need to convert this to centimeters:
h=1m=100cm
The volume V of a cylinder is given by the formula:
V=πr2h
Substituting the values of π, r, and h:
V=227×(25.2)2×100
Calculating (25.2)2:
(25.2)2=635.04
Now substituting this back into the volume formula:
V=227×635.04×100
Calculating 227×635.04:
V=22×90.720=1995.84cm3
Now, since 1cm3=0.001liters:
V=1995.84×0.001=1.99584liters
Rounding 1.99584 to one decimal place gives:
V≈199.6liters
Topper's Solved these Questions
Similar Questions
The circumference of the base of a right circular cone is 44cm and its height is 24 cm. The curved surface area (in cm2) of the cone is :
एक गोलाकार शंकु के आधार की परिधि 44 cm है और इसकी ऊंचाई 24 cm है। शंकु की घुमावदार सतह क्षेत्र (cm2 में) है
View SolutionThe radius of a circular cylinder is 5 cm and its height is 14 cm. Then the volume of cylinder in cm3 is: (Take π=227)
एक गोलाकार बेलन की त्रिज्या 5 सेमी है और इसकी ऊंचाई 14 सेमी है। फिर बेलन का आयतन (cm3 में) है:
View SolutionThe area of the base of a right circular cone is 81πcm2 and its height is 12cm. What is the curved surface area (in cm2) of the cone ?
एक गोलाकार शंकु के आधार का क्षेत्रफल 81πcm2 सेमी है और इसकी ऊंचाई 12 cm है। शंकु का घुमावदार सतह क्षेत्रफल (cm2 में ) क्या है?
View SolutionThe area of the base of a right circular cone is 400π and its height is 15 cm. The curved surface area of the cone (in cm2) is :
एक लम्ब वृत्तीय शंकु के आधार का क्षेत्रफल 400π है और इसकी ऊंचाई 15 सेमी है | इस शंकु का वक्र पृष्ठ क्षेत्रफल ( वर्ग सेमी में ) है :
View SolutionThe circumference of the base of a conical tent is 66 m. If the height of the tent is 36 m, what is the area (in m2) of the canvas used in making the tent? (Take ∏=227)
एक शंक्वाकार तंबू के आधार की परिधि 66 मीटर है | यदि तंबू की ऊंचाई 36 मीटर है, तो उस तिरपाल का क्षेत्रफल ज्ञात करें, जिसका प्रयोग तंबू के निर्माण में किया गया है | (∏=227)
View SolutionA reservoir is in the shape of a frustum of a right circular cone. The radii of its circular ends are 4 m and 8 m and its depth is 7 m. How many kilolitre of water (correct up to one decimal place) can it hold? (π=227)
एक जलाशय किसी लम्ब वृत्तीय शंकु के छिन्नक के आकार का है | इसके वृत्ताकार सिरों की त्रिज्याएँ 4 मी और 8 मी की हैं तथा इसकी गहराई 7 मी है | यह कितने किलोलीटर पानी ( दशमलव के दो स्थान तक ) को धारण कर सकता है ?
View SolutionThe radius of a circular cone is 6 cm and its height is 7 cm. Then the volume of cone in cm3 is: (take π=227)
एक गोलाकार शंकु की त्रिज्या 6 cm है और इसकी ऊंचाई 7 सेमी है। फिर शंकु का आयतन cm3 में क्या होगा ?
View SolutionThe radius of the base of a cylinder is 7 cm and its curved surface area is 440 square cm. Its volume (In cubic cm) will be:(Take π=227)
एक बेलन के आधार की त्रिज्या 7 सेमी है और इसका वक्र पृष्ठीय क्षेत्रफल 440 वर्ग सेमी है। इसका आयतन कितना होगा?
View SolutionThe radius of the base of a cylinder is 14cm and its volume is 6160cm3. The curved surface area (in cm2) of the cylinder is: (Take π=227)
एक सिलेंडर के आधार की त्रिज्या 14 cm है और इसका आयतन 6160cm3 है। सिलेंडर का वक्र पृष्ठीय क्षेत्रफल (cm2 में) क्या है?
View SolutionIn the given histogram,what is the mean height of all students correct to one decimal place? /
दिए गए आयतचित्र में, एक दशमलव स्थान तक सभी छात्रों की औसत लंबाई क्या है?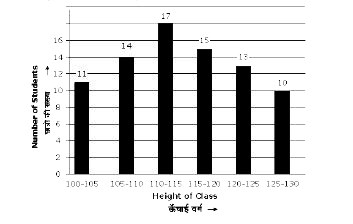
View Solution
