The length of the shadow of the vertical tower on level ground increases by 10m when the altitude of the sun changes from 45∘ to 30∘.The height of the tower is:
समतल भूमि पर खड़ी मीनार की छाया की लंबाई 10 मीटर तक बढ़ जाती है जब सूर्य की ऊँचाई 45∘ से 30∘ तक बदल जाती है। टॉवर की ऊंचाई है:
10(√3+1)m
10√3m
5√3m
5(√3+1)m
To find the height of the tower given that the length of its shadow increases by 10 meters when the altitude of the sun changes from 45 degrees to 30 degrees, we can follow these steps:
Step 1: Define the Variables
Let:
- H = height of the tower
- BC = length of the shadow when the sun is at 45 degrees
- AB = increase in shadow length = 10 m
- AC = total length of the shadow when the sun is at 30 degrees = BC+AB
Step 2: Use the Tangent Function for 45 Degrees
When the sun is at an altitude of 45 degrees, we can use the tangent function:
tan(45∘)=HBC
Since tan(45∘)=1, we have:
H=BC
Step 3: Use the Tangent Function for 30 Degrees
When the sun is at an altitude of 30 degrees, we again use the tangent function:
tan(30∘)=HAC
Since tan(30∘)=1√3, we can write:
1√3=HBC+10
Substituting H from Step 2:
1√3=BCBC+10
Step 4: Cross Multiply to Solve for BC
Cross multiplying gives us:
BC+10=√3⋅BC
Rearranging this, we get:
√3⋅BC−BC=10
Factoring out BC:
BC(√3−1)=10
Thus, we can solve for BC:
BC=10√3−1
Step 5: Rationalize the Denominator
To rationalize the denominator:
BC=10(√3+1)(√3−1)(√3+1)=10(√3+1)3−1=10(√3+1)2=5(√3+1)
Step 6: Conclusion
Since H=BC, the height of the tower is:
H=5(√3+1) meters
Let:
- H = height of the tower
- BC = length of the shadow when the sun is at 45 degrees
- AB = increase in shadow length = 10 m
- AC = total length of the shadow when the sun is at 30 degrees = BC+AB
When the sun is at an altitude of 45 degrees, we can use the tangent function:
tan(45∘)=HBC
Since tan(45∘)=1, we have:
H=BC
When the sun is at an altitude of 30 degrees, we again use the tangent function:
tan(30∘)=HAC
Since tan(30∘)=1√3, we can write:
1√3=HBC+10
Substituting H from Step 2:
1√3=BCBC+10
Cross multiplying gives us:
BC+10=√3⋅BC
Rearranging this, we get:
√3⋅BC−BC=10
Factoring out BC:
BC(√3−1)=10
Thus, we can solve for BC:
BC=10√3−1
To rationalize the denominator:
BC=10(√3+1)(√3−1)(√3+1)=10(√3+1)3−1=10(√3+1)2=5(√3+1)
Since H=BC, the height of the tower is:
H=5(√3+1) meters
Topper's Solved these Questions
Similar Questions
The shadow of a vertical tower on level ground increases by 10 m when the altitude of the sun changes from 45∘ to 30∘. Find the height of the tower.
View SolutionThe shadow of a vertical tower on level ground increases by 10 metres, when the altitude of the sun changes from angle of elevatin 450→300. Find the height of the tower, correct to one place of decimal. (Take√3=1.73
View Solution
Knowledge Check
The shadow of a vertical tower becomes 30 metres longer when the altitude of the sun changes from 60∘to45∘ .find the height of the tower .
A15√3 metresB15(3+√3) metresC15(3−√3) metresD12(3+√3) metresThe shadow of a tower standing on a level plane is found to be 40 m longer when the sun 's altitude is 45∘ , than when it is 60∘ . The height of the tower is
A644 mB66.644 mC54.644 mD76.644 mThe shadow of a tower on ground level is increased by 30 m, when the angle of depression by the sun changes from 60∘ to 30∘. The height of the tower is?
A. 12√3 m
B. 17√3 m
C. 16√3m
D. 15√3 mABBCCDDA
The shadow of a tower standing in a level plane is found to be 18 m shorter when the sun's altitude changes from 30∘ to 45∘. Show that the height of the tower is 9(1+√3)m.
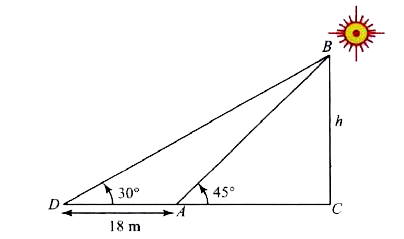
View SolutionThe length of the shadow of a vertical pole on the ground is 18m. If the angle of elevation of the sun at that time is θ , such that cosθ=1213, then what is the height (in m) of the pole?
भूतल पर एक अधोलंब खम्भे की परछाईं की लंबाई 18 मी है। यदि उस समय सूर्य की ऊँचाई का उन्नयन कोण ऐसे है , जैसे कि cosθ=1213 है, तो खम्भे की ऊँचाई (ऊँचाई) क्या है?
View SolutionThe length of the shadow of a vertical pole on the ground is 36m. If the angle of elevation of the sun at that time is θ , such that secθ=1312,then what is the height (in m ) of the pole ?
भूतल पर एक अधोलंब खम्भे की परछाईं की लंबाई 36 मी है। यदि उस समय सूर्य की ऊँचाई का उन्नयन कोण ऐसे है , जैसे कि secθ=1312 है, तो खम्भे की ऊँचाई (ऊँचाई) क्या है?
View SolutionThe length of the shadow of a vertical pole on the ground is 24m. If the angle of elevation of the sun at that time is θ, such that sinθ=513, then what is the height of the pole? /
एक लंबवत खंभे की भूमि पर परछाई की लंबाई 24 मीटर है | यदि उस समय सूर्य के उन्नयन का कोण θ इस प्रकार है कि sinθ=513 है, तो खंभे की ऊंचाई ज्ञात करें |
View SolutionThe angle of elevation of a tower from a distance 100 m from its foot is 30∘ .Height of the tower is :
View Solution
