A hunter is at (4,-1,5) units. He observes two preys at P1(−1,2,0) and P2(1,1,4) respectively. At zero instant he starts moving in the plane of three positions with uniform speed of 5unit−1 in a direction perpendicular to line P1P2 till he sees P1 and P2 collinear at time T.Time T is

0.53s
0.73s
0.35s
0.92s
The correct Answer is:A
→A=−5ˆi+3ˆi−5ˆk,→B=2ˆi−ˆj+4ˆk,R=∣∣→A∣∣sinθ, sinθ=∣∣→A×→B∣∣AB
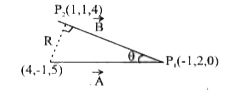
As ∣∣→A×→B∣∣=12.25[∴→A×→B=7ˆi+10ˆj−ˆk] ∴∣∣→B∣∣=4.58
i.e. R=A∣∣→A×→B∣∣AB=∣∣→A×→B∣∣→B∴R=2.67m
Time taken to reach the destination =Rv=0.53s
Similar Questions
A biard is at a point P(4m,−1m,5m) and sees two points P1(−1m,−1m,0m) and P2(3m,−1m,−3m). At time t=0, it starts flying in a plane of the three positions, with a constant speed of 2m/s in a direction perpendicular to the straight line P1P2 till it sees P1 & P2 collinear at time t. Find the time t.
View SolutionA biard is at a point P(4m,−1m,5m) and sees two points P1(−1m,−1m,0m) and P2(3m,−1m,−3m). At time t=0, it starts flying in a plane of the three positions, with a constant speed of 2m/s in a direction perpendicular to the straight line P1P2 till it sees P1 & P2 collinear at time t. Find the time t.
View Solution
Knowledge Check
- Question 1 - Select One
P1:x+3y−z=0andP2:y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2

The angle between P1andP2 is ________.Acos−1(15)Bcos−1(1√55)Ccos−1(2√11)Dcos−1(3√11) - Question 2 - Select One
Let P1:x−2y+3z=5andP2:2x−3y+z+4=0 be two planes. The equation of the plane perpendicular to the line of intersection to the line of intersection of P1=0 and P2= and passing through (1,1,1) is
A11x−5y+7z−13=0B7x+5y+z=13Cx+2y+z−4=0Dx−2t+4z+3=0 - Question 3 - Select One
Question Stimulus :-
If three points (p+1, 1), (2p+1, 3) and (2p+2, 2p) are collinear, then p=?A−1B1C2D0
If p1,p2 and p3 and are respectively the perpendiculars from the vertices of a triangle to the opposite sides, then 1p1+1p2−1p3=.
View SolutionP1,P2 are points on either of the two lines y−√3|x|=2 at a distance of 5 units from the poinföf intersection. Find the coordinates of the foot of perpendiculars drawn from P1,P2 on the bisector the angle between the given lines.
View SolutionLet n1,n2,n3,n4 be vectors normal to the planes p1,P2P3,P4 respectively, then the vector perpendicular to the lines of intersection of p1andp2,andp3andp4, is
View SolutionPoints (P- 1, P+2),(P,P+1),(P+1,P) are collinear
View SolutionP1:x+3y−z=0andP2,y+2z=0 are two intersecting planes P3 is a plane passing through the point (2,1,-1) and through the line of intersection of P1andP2
Equation of P3 isView Solution

