The vectors −−→AB=3ˆi+4ˆk and −−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC. The length of the median through A is
√18
√72
√33
√288
The correct Answer is:C
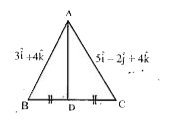
−−→AD=−−→AB+−−→AC2=4ˆi−ˆj+4ˆk ∴∣∣∣−−→AD∣∣∣=√33
Similar Questions
If the vectors −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC, then the length of the median through A is (A) √18 (B) √72 (C) sqrt(33)(D)sqrt(45)
View SolutionIf the vectors −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC, then the length of the median through A is (A) √33 (B) √45 (C) √18 (D) √720
View Solution
Knowledge Check
The vectors −−→AB=3ˆi+5ˆj+4ˆk and −−→AC=5ˆi−5ˆj+2ˆk are the sides of a triangle ABC. The length of the median through A is :
A√13unitB2√5 unitC5 unitD10 unitThe vectors −−→AB=3ˆi+5ˆj+4ˆk and −−→AC=5ˆi−5ˆj+2ˆk are the sides of a triangle ABC. The length of the median through A is :
A√13unitB2√5 unitC5 unitD10 unitIf the vector AB=3ˆi+4ˆk and AC=5ˆi−2ˆj+4ˆk are the sides of a ΔABC then the length of the median through A is
A√18B√72C√33D√288
If the vectors −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC, then the length of the median through A is (A) √33 (B) √45 (C) √18 (D) √720
View SolutionThe vector −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are sides of a triangle ABC. The length of the median through A is (A) √18 (B) √72 (C) √33 (D) √288
View SolutionThe vector −−→AB=3ˆi+4ˆkand−−→AC=5ˆi−2ˆj+4ˆk are sides of a triangle ABC. The length of the median through A is (A) √18 (B) √72 (C) √33 (D) √288
View SolutionThe vector ¯¯¯AB=3ˆi+4ˆk and ove→owAC=5ˆi−2ˆj+4ˆk are the sides of a triangle ABC. The length of the median through A is
View SolutionIf the vectors AB=3ˆi+4ˆk and AC=5ˆi−2ˆj+4ˆk are the sides of a Δ ABC, then the length of the median through A is
View Solution
