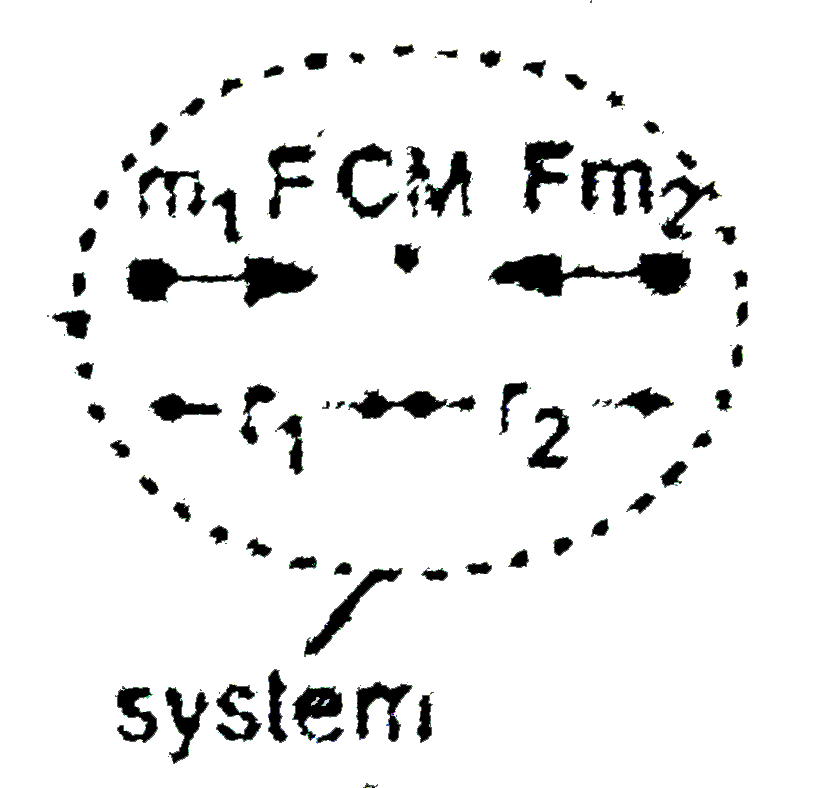
Two particles of masses m, and m, separated by a distance dare at rest initially. If they move towards each other under mutual interaction (say electric, gravitational or elastic), where will they meet?

A

At the centre of the joining the two particles

B

Anywhere in between two masses

C

At the centre of mass of the system of two particles

D

None of the above

Text Solution

Verified by Experts

The correct Answer is:C

Initially, the particles are at fest, so the velocity of the centre of mass,
${\to v}_{C M} = \frac{m_{1} \times 0 + m_{2} \times 0}{m_{1} + m_{2}} = 0,$ As here ${\to F}_{ext} = 0$ so , ${\to v}_{C M}$ = constant
ie, $\frac{m_{1} {\to v}_{1} + m_{2} {\to v}_{2}}{m_{1} + m_{2}} = 0$ (at all instants) or $m_{1} + {\to m}_{1} {\to v}_{1} + m_{2} {\to v}_{2} = 0$
or $m_{t} \frac{Δ {\to r}_{1}}{Δ t} + m_{2} \frac{Δ {\to r}_{2}}{Δ t} = 0$
$m_{1} Δ {\to r}_{1} + m_{2} Δ {\to r}_{2} = 0 (a s Δ t \neq \infty)$
$m_{1} {\to d}_{1} + m_{2} {\to d}_{2} = 0$ (with $Δ \to r = \to d$ )
$m_{1} d_{1} - m_{2} d_{2} = 0$ (as direction ${\to d}_{2}$ is opposite to $d_{1}$ ) or $m_{1} d_{1} = m_{2} d_{2}$
But given that $d_{1} + d_{2} = d$ so that $d_{1} = \frac{m_{2} d}{m_{1} + m_{2}} and d_{2} = \frac{m_{1} d}{m_{1} + m_{2}}$
Now, as $d_{1} and d_{2}$ represent the position of the centre of the mass relative to $m_{1} and m_{2}$ respectively the particles will collide at the centre of mass of the system,

|

Updated on:21/07/2023

Class 11 PHYSICS MOTION OF SYSTEMS OF PARTICLES AND RIGID BODY

Similar Questions

Knowledge Check

Question 1 - Select One
When two blocks connected by a spring move towards each other under mutual interaction
A(a) their velocities are equal
B(b) their accelerations are equal
C(c) the force acting on them are equal and opposite
D(d) All of the above
Question 2 - Select One or More
When two blocks connected by a spring move towards each other under mutual interaction,
A(a) Their velocities are equal and opposite
B(b) Their accelerations are equal and opposite
C(c) The forces acting on them are equal and opposite
D(d) Their momenta are equal and opposite
Question 3 - Select One
Two particles of masses $4 k g$ and 6kg $a r e s e p a r a t e d b y a d i s tan c e o f$ 20cm and are moving towards each other under mutual force of attraction, the position of the point where they meet is
A $12 m$ from $4 k g$ body
B $12 m$ from $6 k g$ body
C $8 m$ from $4 k g$ body
D $10 m$ from $4 k g$ body

Recommended Questions

Home
Ask Doubt
Profile