Two particles of equal mass m each , go round a circle of radius R, under the action of their mutual gravitational attraction. The speed of each particle is
√Gm2R
12R√1Gm
12√GmR
√2GmR
The correct Answer is:C
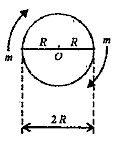
Centripetal force = Gravitational force or mv2R=Gm×m(2R)2
or v2=Gm4Rorv=12√GmR
Similar Questions
Two particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
View SolutionTwo particles of equal masses m go round a circle of radius R under the action of their mutual gravitational attraction. The speed of each particle is v=√GmnR. Find the value of n.
View Solution
Knowledge Check
Two particles of equal mass m go around a circle of radius R under the action the of their mutual gravitational attraction . The speed v of each particle is
A12√GmRB√4GMRC12R√1GmD√Gm2RTwo particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of each particle is
A12R√(1Gm)B√(Gm2R)C12√(GmR)D√(4GmR)Two particles of equal mass go around a circle of radius R under the action of their mutual gravitational attraction. The speed v of earth particle is
A13√GmRB12√GmRC12√RGmD√GmR
Two particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass go round a circle of radius R under the action of their mutual gravitational attraction. Find the speed of each particle.
View SolutionTwo particles of equal mass 'm' go around a circle of radius R under the action of their mutual gravitaitonal attraction. The speed of each particle with respect to their centre of a mass is -
View SolutionTwo identical particles of mass 1 kg each go round a circle of radius R, under the action of their mutual gravitational attraction. The angular speed of each particle is :
View SolutionTwo particles of equal mass m go around a circle of radius R under action of their mutual gravitational attraction. The speed of each particle with respect to their centre of mass is
View Solution
