A sphere of radius $0.1 m$ and mass $8 π k g$ is attached to the lower end of a steel wire of length $5.0 m$ and diameter $10^{- 3} m$ . The wire is suspended from $5.22 m$ high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lower point. Calculate the velocity of the sphere at the lowest position . Y for steel $= 1.994 \times 10^{11} N / m^{2}$ .

Text Solution

Verified by Experts

As the length of the wire is $5 m$ and diameter of sphere $2 \times 0.1 = 0.2 m$ and at lowest point it grazes the floor which is at a distance $5.22 m$ from the roof, the increase in length of the wire at lowest point

$Δ L = 5.22 - (5 + 0.2) = 0.02 m$
So tension in the wire (due to elasticity)
$T = \frac{Y A}{L} Δ L = \frac{1.994 \times 10^{11} \times π {(5 \times 10^{- 4})}^{2} \times 0.02}{5} = 199.4 π N$
and as equation of circular motion of a mass m tied to a string in a vertical plane is
$(m v^{2} / r) = T - m g cos θ$
So, at lowest point
$(m v^{2} / r) = T - m g$ [as $θ = 0$ ]
But here $r = 5 + 0.02 + 0.1 = 5.12 m$
So, $(8 π v^{2} / 5.12) = (109.4 π - 8 π \times 9.8)$
i.e., $v^{2} = (121 \times 5.12 / 8) = 77.44$
So, $v = 8.8 m s / s$

Updated on:21/07/2023

A sphere of radius $0.1 m$ and mass $8 π$ $k g$ is attached to the lower end of a steel wire of length $5.0 m$ and diameter $10^{- 3} m$ . The wire is suspended from $5.22 m$ high ceiling of a room . When the sphere is made to swing as a simple pendulum, it just grazes the floor at its lowest point. Calculate the velocity of the sphere at the lowest position . Young's modulus of steel is $(1.994 \times 10^{11} N / m^{2})$ .
A $7.7 m s^{- 1}$
B $4.4 m s^{- 1}$
C $2.2 m s^{- 1}$
D $8.8 m s^{- 1}$
A sphere of mass $m$ attached with the free end of a steel wire of length $l$ swings in the veritical plane form the horizontal positon.

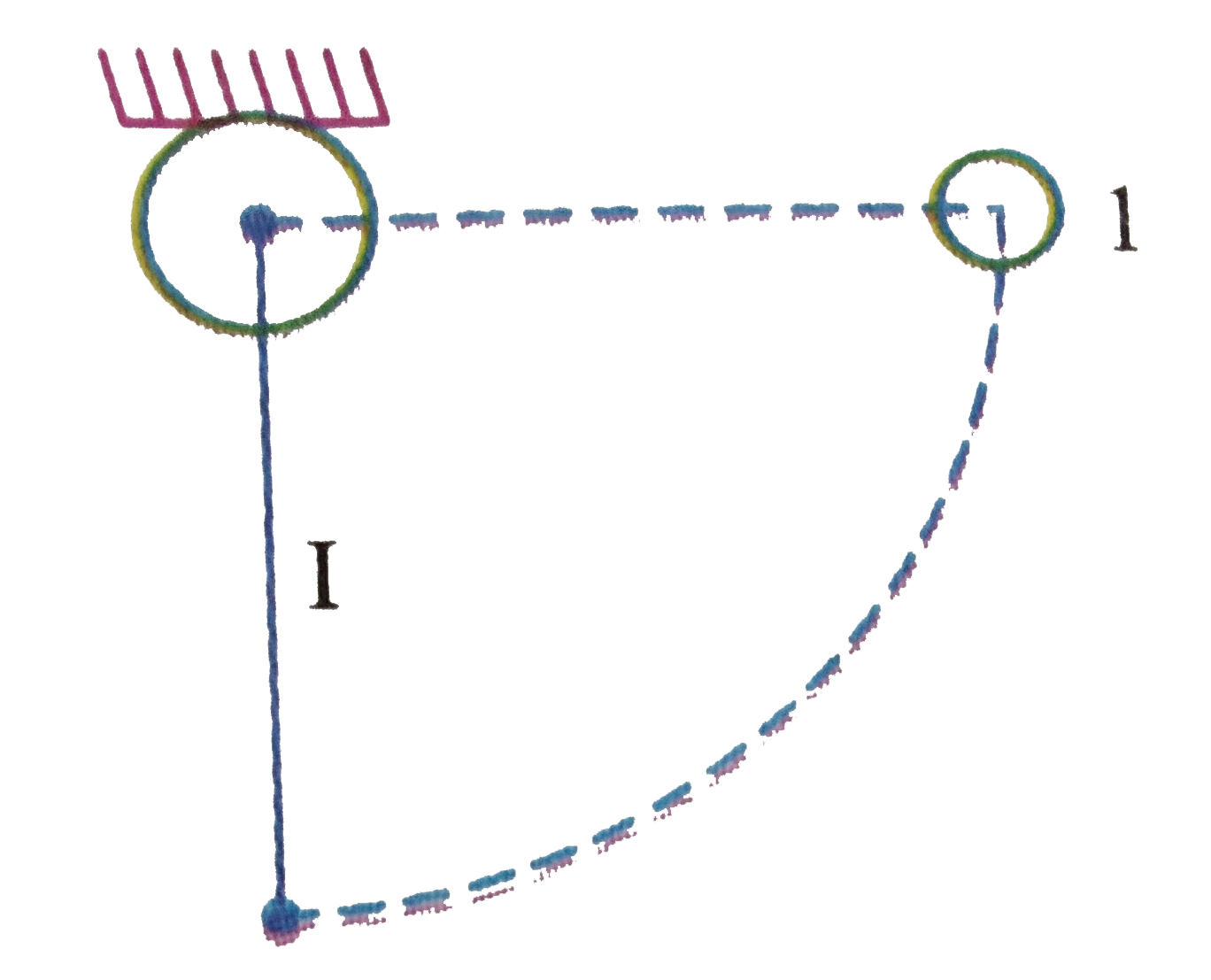
Elongation of the wire in the vericle positon is
A $\frac{m g l}{Y (π r^{2})}$
B $\frac{2 m g l}{Y (π r^{2})}$
C $\frac{m g l}{3 Y (π r^{2})}$
D $\frac{3 m g l}{Y (π r^{2})}$
A sphere of mass $m$ attached with the free end of a steel wire of length $l$ swings in the veritcle plane form the horizontal positon.

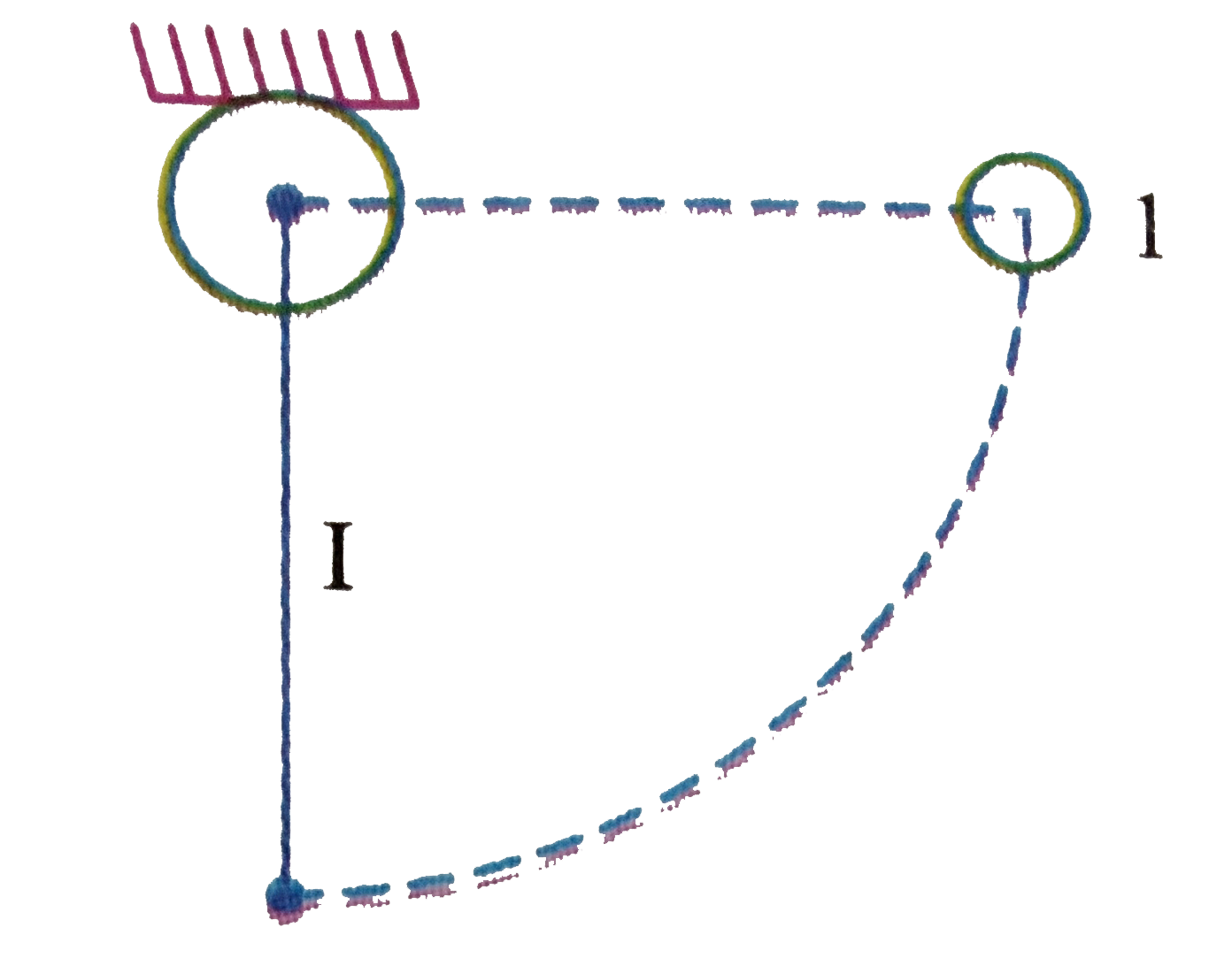
Elastic energy should in the wire in the vericle positon is
A $\frac{9 m^{2} g^{2} l}{2 Y π r^{2}}$
B $\frac{7 m^{2} g^{2} l}{2 Y π r^{2}}$
C $\frac{9 m^{2} g^{2} l}{Y π r^{2}}$
D $\frac{9 m^{2} g^{2} l}{4 Y π r^{2}}$