A capillary tube is immersed vertically in water and the height of the water column is x. When this arrangement is taken into a mine of depth d, the height of the water column is y. If R is the radius of the earth, the ratio xy is
(1−dR)
(1+dR)
(R−dR+d)
(R+dR−d)
The correct Answer is:A
On earth.s surface, σ=xρrg2
In the time, σ=yρrgd2 , Dividing we get xy=gdg=g(1−dR)g=1−dR
Similar Questions
The lower end of a glass capillary tube is dipped in water. Water rises to a height of 9 cm. The tube is then broken at a height of 5 cm. The height of the water column and angle of contact will be
View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opened again. The length of the water column remaining in the tube will be
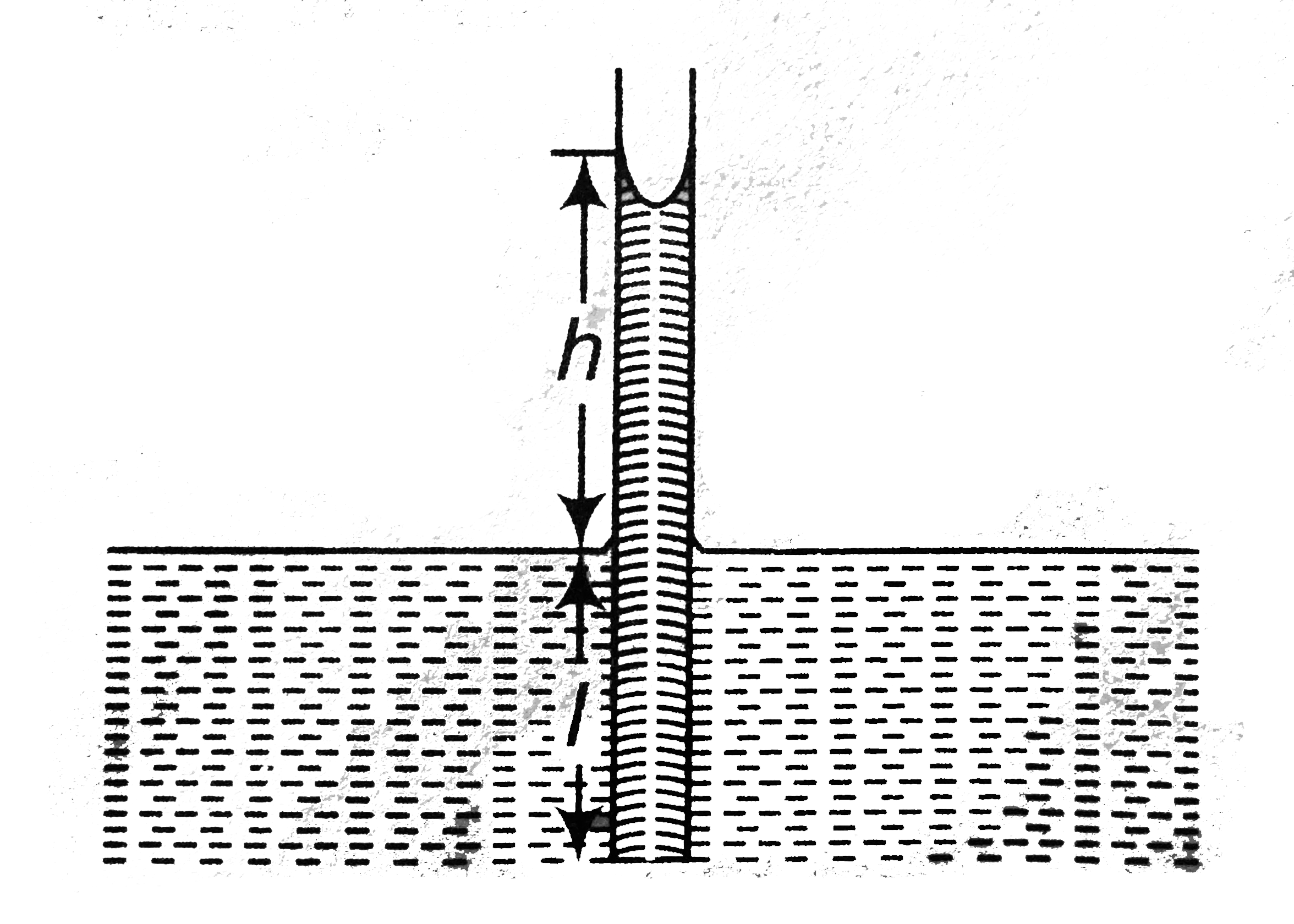 .
.
View Solution
Knowledge Check
A capillary tube is immersed vertically in water such that the height of liquid column is found to be x on the surface of the earth. When it is taken to mine the capillary rise is y if R is the radius of the earth. Then the depth of mine is
Ad=R(y−x)xBd=R(y−x)yCd=R(xy−x)Dd=R(yy−x)Water rises upto a height x in capillary tube immersed vertically in water . When this whole arrangement is taken to a depth d in a mine , the water level rises upto a height y . If R is the radius of the earth , then the ration xy is given by
A1+dRB1−dRCR+dR−dDR−dR+dIf a capillary tube of diameter 0.4 m is dipped vertically into water, then the height to which water rises in the capillary tube will be ,
A7.143 cmB0.013 cmC714.3 cmD7143 cm s
When two capillary tubes A and B are immersed in water , the heights of water columns are found to be in the ratio 2:3 the ratio of the radii of tubes A and B is
View SolutionThe lower end of a glass capillary tube is dipped in water. Water rises to a height of 9 cm. The tube is then broken at a height of 5 cm. the height of the water column and angle of contact will be
View SolutionThe lower end of a glass capillary tube is dipped in water. Water rises to a height of 9 cm. The tube is then broken at a height of 5 cm. The height of the water column and angle of contact will be
View SolutionWater rises to a height h in a capillary tube lowered vertically into water to a depth l as shown in the figure. The lower end of the tube is now closed, the tube is the taken out of the water and opend again. The length of the eater column remaining in the tube will be
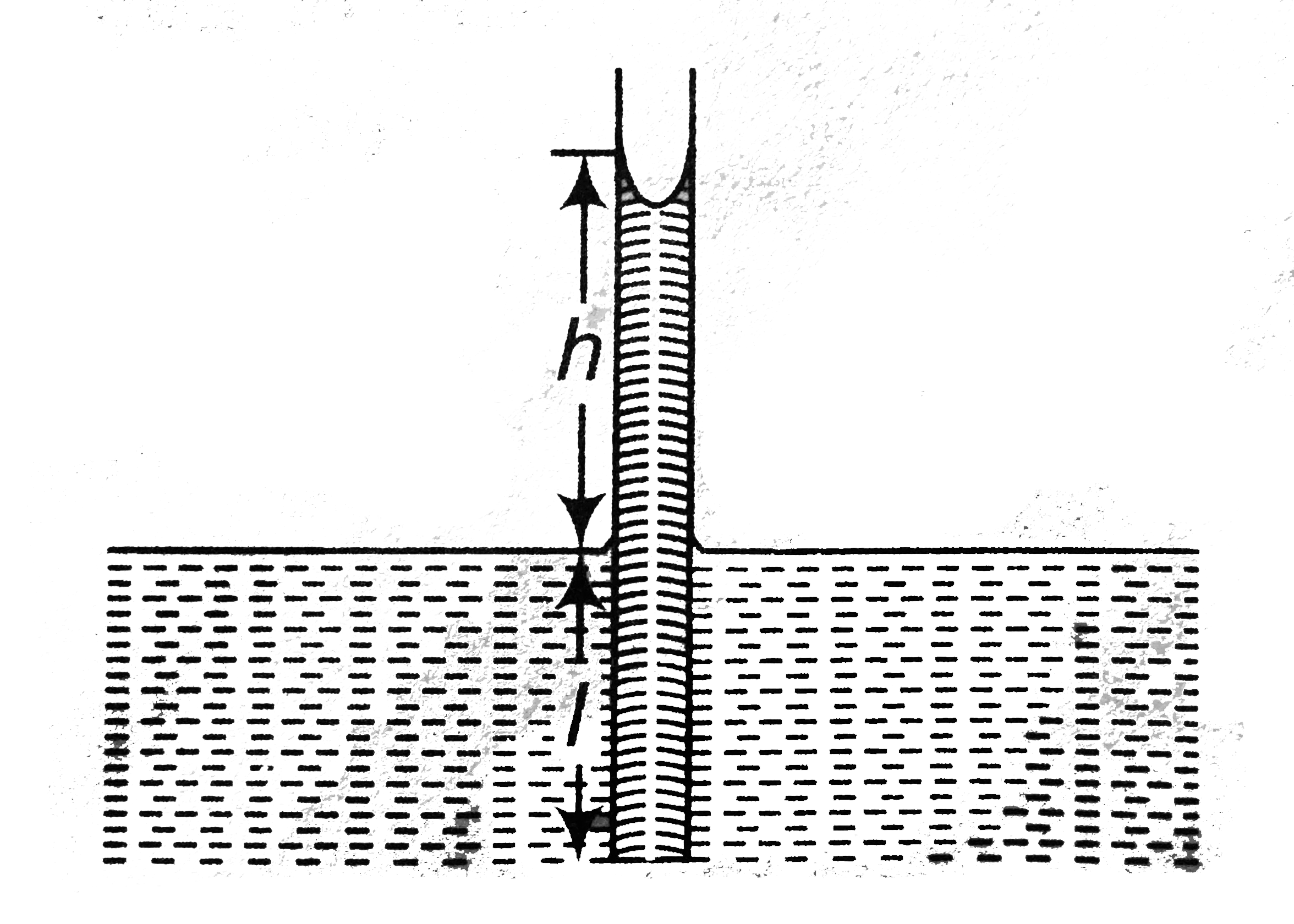 .
.
View SolutionWater rises upto 10 cm height in a long capillary tube. If this tube is immersed in water so that the height above the water surface is only 8 cm, then
View Solution
