A bird in air is diving vertically over a tank with speed 6 cm/s. The base of the tank is silvered. The fish in the tank is rising upward along the same line with speed 4 cm/s. [Take : μwater=43] Find : (A) The speed of the image of the fish as seen directly by the bird. (B) The speed of the image of the bird relative to the fish looking upwards.
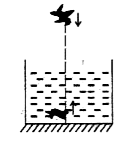
(A) Velocity of the image of fish in air =4×34=3↑⏐
⏐⏐
Velocity of image of fish w.r.t. bird =3+6=9↑
(B) Velocity of image of bird in water =6×43=8⏐⏐
⏐↓
Velocity of image of bird w.r.t. fish =8+4=12↓
Similar Questions
A bird in air is dividing vertically over a tank with speed 6cm/s. The base of the tank is silvered. The fish in the tank is rising upward along the same line with speed 4cm/s. (Take: μwater=4/3). Find:
(a) The speed of the image of the fish asseen directly by the bird.
(b) The speed of the image of the bird relative to the fish looking upwards.
View SolutionA bird in air is diving vertically over a tank with speed 6 cm//s Base of the tank is silvered A fish in the tank is rising upward along the same line with speed 4 cm//s[Take:mu_(water)=4//3]

Column-IColumn-II(A)Speed of the image of fish as seen by the bird directly(P)12(B) Speed of the image of fish formed after reflectionfrom the mirror as seen by the bird(Q) 4(C)Speed of image of bird relative to the fish looking upwards(R) 9(D) Speed of image of bird relative to the fish lookingdownwards in the mirror(S) 3
View Solution
Knowledge Check
In the previous question, if the bird is diving vertically down with speed =6m/s , his appearent speed as seen by a stationary fish underwater is
A8m/sB6m/sC12m/sD4m/sA bird is flying 3m above the surface of water,If the bird is diving vertically down with speed =6m/shis apparent velocity as seen by a stationary fish underwater is:
A8m/sB6m/sC12m/sD4m/sA bird in air looks at a fish vertically below it and inside water. h1 is the height of the bird above the surface of water and h2, the depth of the fish below the surface of water. If refractive index of water with respect to air be μ, then the distance of the fish as observed by the bird is
Ah1+h2Bh1+h2μCμh1+h2Dμh1+μh2
A bird B in air is diving vertically downwards over a water tank with speed 5 cm/s. Base of the tank is silvered. A fish F in the tank is rising vertically upwards along the same line with speed 2 cm/s. Water level is lowered at the rate of 2 cm/s. Take μwater=4/3
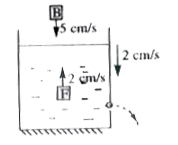
View SolutionA bird in air is diving vertically over a tank with speed 5cm//s , base of tank is silvered. A fish in the tank is rising upward abong the same line with speed 2cm/s. Water level is falling at rate of 2cm/s [Take :μwater=4/3]
_S01_069_Q01.png)
ColumnI(cm/s)ColumnII(A)Speed of the image of fish as seen by the bird directly(P)8(B)Speed of the image of fish formed after reflection in the mirror as seen by the bird(Q)6(C)Speed of image of bird relative to the fish looking upwards(R)3(D)Speed of image of bird relative to the fish looking downwards in the mirror(S)4
View SolutionFind out the following in the figure shown below :
(a) The apparent speed of the fish as observed by the bird
(b) The apparent speed of the bird as observed by the fish
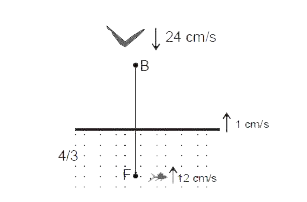
View SolutionA fish is 60 cm under water (μ=4/3). A bird directly overhead looks at the fish. If the bird is at a distance of 120 cm from the water surface, (a) What is the apparent position of the fish as seen by the bird and (b) what is the apparent position of the bird as seen by the fish?
View SolutionDaniel walks directly toward a plane mirror at a speed of 0.25ms. Determine the speed of the image relative to him.
View Solution
