A spherical surface of radius of curvature R separates air(refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point and PO-OQ. The distance PO is equal to 

A

5 R

B

3R

C

2R

D

1.5 R

Text Solution
Verified by Experts

The correct Answer is:A

ocr_image
By using μ 2 v - μ 1 u = μ 2 - μ 1 R
μ 1 = 1 , μ 2 = 1.5 , u = - O P , v = O Q
Hence 1.5 O Q - 1 - O P = 1.5 - 1 ( + R ) , O P = 5 R

Updated on:21/07/2023
Doubtnut Promotions Banner
|
Class 12PHYSICSGEOMETRICAL OPTICS

Similar Questions

Knowledge Check

  • A spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The centre of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The line PQ cuts the surface at a point O, and PO=OQ. The distance PO

    A5R
    B3R
    C2R
    D1.5R

  • A spherical surface of radius of curvature R separates air (refractive index 1.0) from glass (refractive index 1.5). The center of curvature is in the glass. A point object P placed in air is found to have a real image Q in the glass. The ling PQ cuts the surface at a point O, and PO=OQ. The distance PO is equal to

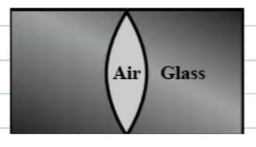
    A5R
    B3R
    C2R
    D1.5R

  • In figure, an air lens of radius of curvature of each surface equal to 10cm is cut into a cylinder of glass of refractive index 1.5. The focal length and the nature of lens are
    ocr_image

    A15cm diverging
    B15cm converging
    C10cm diverging
    D10cm converging