The light is incident at an angle 60∘ on a prism of which the refracting angle of prism is 30∘. The refractive index of material of prism will be
√2
2√3
2
√3
The correct Answer is:D
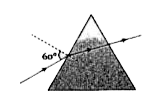
By using i + e = A+δ, 60+e=30+30, e=0
Hence ray will emerge out normally so by using the formula μ=sinisinA=sin60sin30=√3
Similar Questions
The angle of minimum deviation measured with a prism is 30∘ and the angle of prism is 60∘. The refractive index of prism material is
View Solution(a) If the refracting angle of a prism is 60∘ and the minimum deviation is 30∘, then find the angle of incidence.
(b) A ray of light passes through an equilateral prism such that the angle of emergence is equal to the angle of incidence and each is equal to 3/4th of the angle of prism. Find the angle of deviation.
(c) The refracting of a prism is A and the refractive index of the material of the prism is cotA/2. Find the angle of deviation.
(d) The angle of a prism is 60∘. What is the angle of incidence for minimum deviation? The refractive index of the material of the prism is √2.
View Solution
Knowledge Check
A ray of light is incident at an angle of 60∘ on the face of a prism with an angle of 60∘. Then the refractive index of the material of the prism is (the prism is in minimum deviation position)
A1.414B1.623C1.524D1.732A trihedral prism with refracting angle 60∘ deviates a light ray by 30∘. The refractive index of the material of prism
Amay be equal to √2Bcan not be greater than √2Ccan not be less than √2Dnone of theseThe angle of minimum deviation measured with a prism is 30∘ and the angle of prism is 60∘. The refractive index of prism material is
A√2B2C3/2D4/3
A ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionA ray of light incident at an angle 90° with the face of an equilateral prism passes symmetrically. Calculate the refractive index of the material of the prism
View SolutionA ray of light incident at an angle of 48∘ is refracted through a prism in its position of minimum deviation. The angle of prism is 60∘. Calculate the refractive index of the material of the prism. (sin48∘=0.74,sin30∘=0.50)
View SolutionThe angle of minimum deviation measured with a prism is 30∘ and the angle of prism is 60∘ . The refractive index of the prism material is
View SolutionA ray of light incident on a prism of angle 60∘, does not emerge out. Refractive index of material of prism may be
View Solution
