The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. Ifa concave lens of focal length 20 cm is placed between the convex lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image
1.25 cm
2.5 cm
1.05 cm
2 cm
The correct Answer is:B
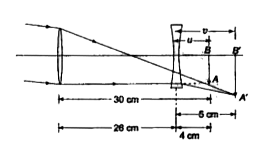
AB is the image of size 2 cm formed by the convex lens at its focal plane. It serves as the virtual object for the concave lens. A.B. is the final image. For concave lens, f = -20 cm, u = +4 cm.
1v−1u=1f or 1v−14=−120
which gives v = 5 cm. Thus the final image at a distance of 5 cm from the concave lens.
Now A.B.AB=vu or A.B.2cm=5cm4cm or A.B. = 2.5 cm.
Similar Questions
A convex lens of focal length 30 cm forms an image of height 2 cm for an object situated at infinity. If a concave lens of focal length 20 cm is placed coaxially at a distance of 26 cm from convex lens then size of image would be
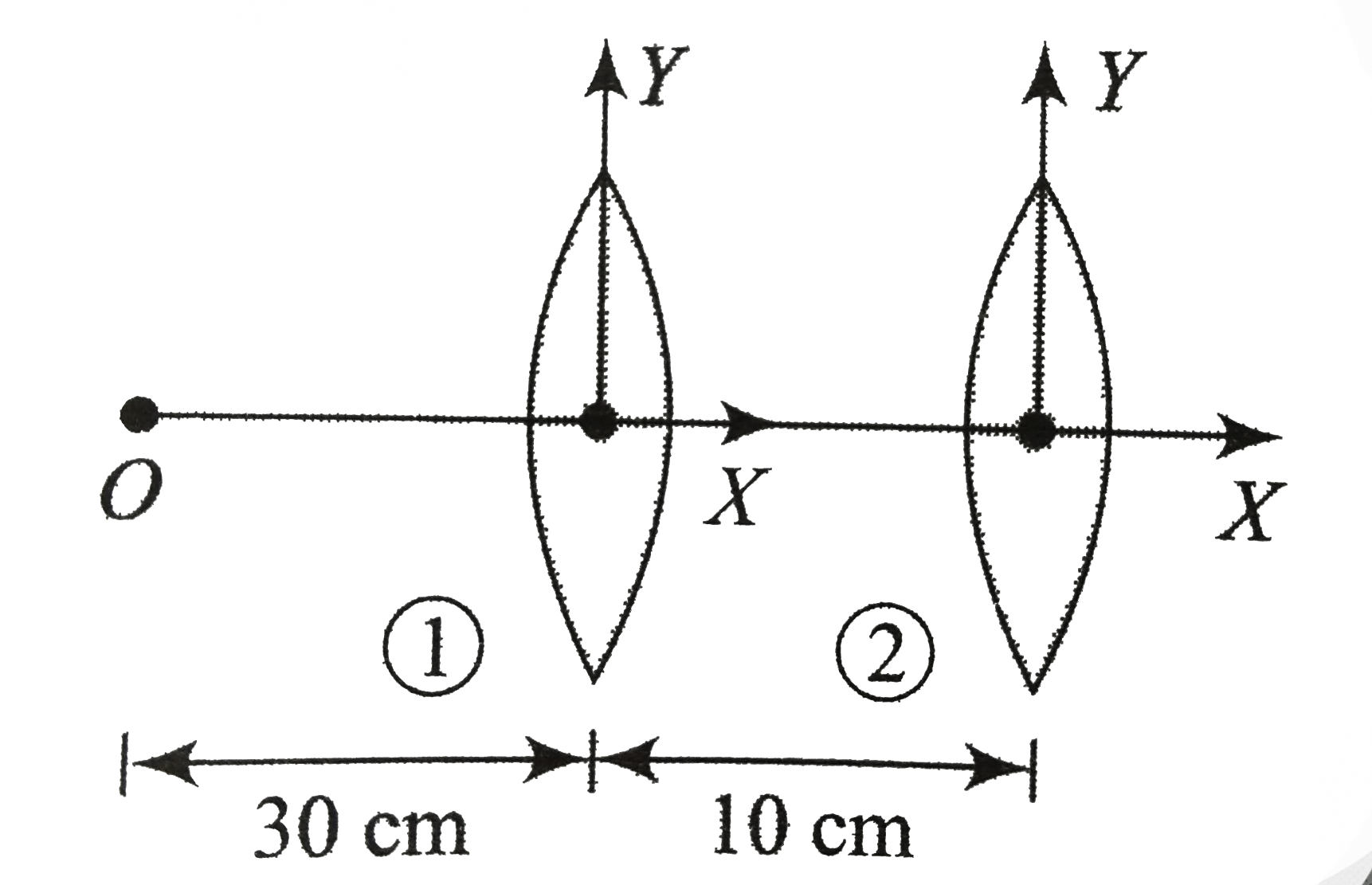
View SolutionA convex lens of focal length 20cm is placed 10cm away from a second convex lens of focal length 25 cm. What wil be the location of the image of an object at 30 cm in front of the first lens?
View Solution
Knowledge Check
The size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30cm is 2cm. If a concave lens of focal length 20cm is placed between the convex lens and the image at a distance of 26cm from the convex lens, calculate the new size of the image.
A1.25cmB2.5cmC1.05cmD2cmThe size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convex lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image.
A1.25cmB2.5cmC1.05cmD2cmThe size of the image of an object, which is at infinity, as formed by a convex lens of focal length 30 cm is 2 cm. If a concave lens of focal length 20 cm is placed between the convax lens and the image at a distance of 26 cm from the convex lens, calculate the new size of the image.
A1.25cmB2.5cmC1.05cmD2cm
A convex lens of focal length 20cm is placed 10cm away from a second convex lens of focal length 25 cm. What wil be the location of the image of an object at 30 cm in front of the first lens?

View SolutionAn object is placed at a distance of 30 cm from a convex lens of focal length 20 cm.Find the position of the image .
View SolutionThe size of the image of an object,which is at infinity, as formed by a convex lens of focal length 20 cm is placed between the convex lens and the image at the distance of 26 cm from the convex lens, the new size of the image is
View SolutionA convex lens of focal length 30 cm forms an image of height 2 cm for an object situated at infinity. If a concave lens of focal length 20 cm is placed coaxially at a distance of 26 cm from convex lens then size of image would be
View SolutionA convex lens of focal length 16 cm forms a real image double the size of the object. The image distance of the object from the lens is
View Solution
