If the distance between a point source and a screen is doubled, then intensity of light on the screen will become
Four times
Double
Half
One-fourth
The correct Answer is:D
Intensity of light at a point is inversely proportional to square of the distance of the point from source of light.
I∝1[distance (d)]2,I1I2=[d2d1]2=41⇒I2=I14
Similar Questions
A source of light is placed in front of a screen. Intensity of light on the screen is I. Two Polaroids P1 and P2 are so placed in between the source of light and screen that the intensity of light on screen is I/2.P2 should be rotated by an angle of (degrees) so that the intensity of light on the screen becomes 3I8
View SolutionA source S is kept directly behind the slit S1 in a double slit apparatus. What will be the phase difference at P, if a liquid of refraction index μis filled : (wavelength of light in aire is λ due to the source, assume l>>d,D>>d).
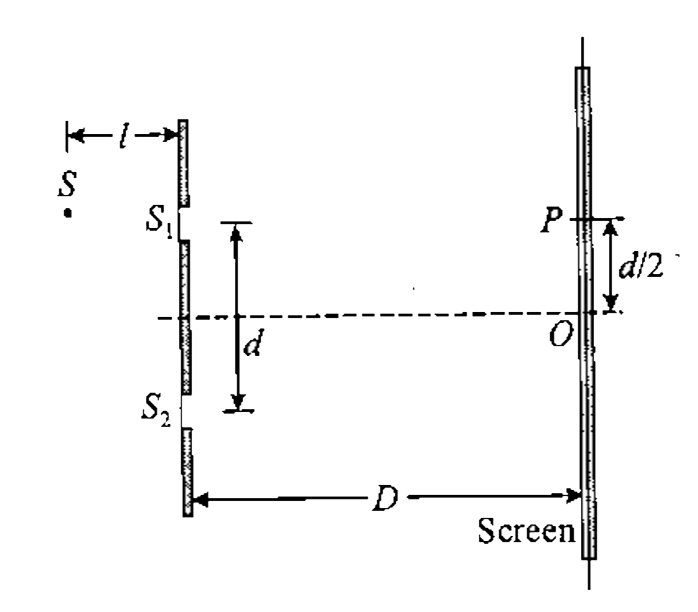
(a) Between the screen and the slits.
(b) Between the slits & the source S. In this case, find the minimum distance between the points on the screen where the intensity is half the maximum intensity on the screen.
View Solution
Knowledge Check
If the distance between a point source and screen is doubled, then intensity of light on the screen will become
AFour timesBDoubleCHalfDOne-fourthIn a cinema hall, the distance between the projector and the screen in increased by 2% . Then the intensity of illumination on the screen is
Adecreased by 2%Bdecreased by 4%Cincreased by 2%Dincreased by 4%The distance between a point source of light and a screen which is 60 cm is increased to 180 cm . The intensity on the screen as compared with the original intensity will be
A(1/9) timesB(1/3) timesC3 timesD9 times
A source S is kept directly behind the slit S1 in a double slit apparatus. What will be the phase difference at P, if a liquid of refraction index μis filled : (wavelength of light in aire is λ due to the source, assume l>>d,D>>d).

(a) Between the screen and the slits.
(b) Between the slits & the source S. In this case, find the minimum distance between the points on the screen where the intensity is half the maximum intensity on the screen.
View SolutionA point source of light 'S' at a distance d from the screen A produces light intensity I0 at the centre of the screen. If a completely reflecting mirror M is placed at a distance d behind the source as shown in the figure, find the intensity at the centre of the screen

View SolutionIn young's double slit experiment, if the distance between the slits is halved and the distance between the slits and the screen is doubled, the fringe width becomes
View SolutionIn Young's double slit experiment, the distance between the two slits is 0.1 mm, the distance between the slits and the screen is 1 m and the wavelength of the light used is 600 nm. The intensity at a point on the screen is 75% of the maximum intensity. What is the smallest distance of this point from the central fringe ?
View SolutionIn Young's double-slit experiment using λ=6000Å, distance between the screen and the source is 1m. If the fringe-width on the screen is 0.06 cm, the distance between the two coherent sources is
View Solution
