Two coaxial loops of radii 0.5 m and 0.05 m are separated by distance 0.5 m and carry currents 2 A and 1 A respectively. What is the force between the loops
As shown in figure, the field due to coil C1 at the centre of C2,¯¯¯B1=μ04π2πR21(R21+x2)3/2(¯i)
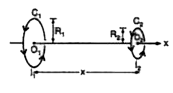
and as the magnetic moment of coil C2
¯¯¯¯M2=I2¯¯¯S2=I2πR22(¯i)
and as its radius R2<<x so treating it as a dipole in the field of coil C1, its potential energy
U=−¯¯¯¯M2.¯¯¯B1=μ04π2π2R21R22I1I2(R21+x2)3/2 [as¯i.¯i=1]
and hence the force between the coils C1andC2
F=−DUdx=μ04π(2π2R21R22I1I2)ddx[(R21+x2)−3/2]
i.e., F=−μ04π6π2R21R22I1I2x(R21+x2)5/2.....(82)
So, F=−10−76π2×(0.5)2×(0.05)2×1×2×(0.5)[(0.5)2+(0.5)2]5/2=−2.09×10−8N
The negative sign here implies that the force is attractive and if the current in the two coils had been in opposite directions the force will be positive i.e., repulsive, which is in accordance with the fact that similar currents attracts while oppsite repel
Similar Questions
Two coaxial circular loops of raadii r1 and r2 are separated by a distance x and carry currents i1 and i2 respectively. Calculate the mutual inductance. What is the force between the loops ?
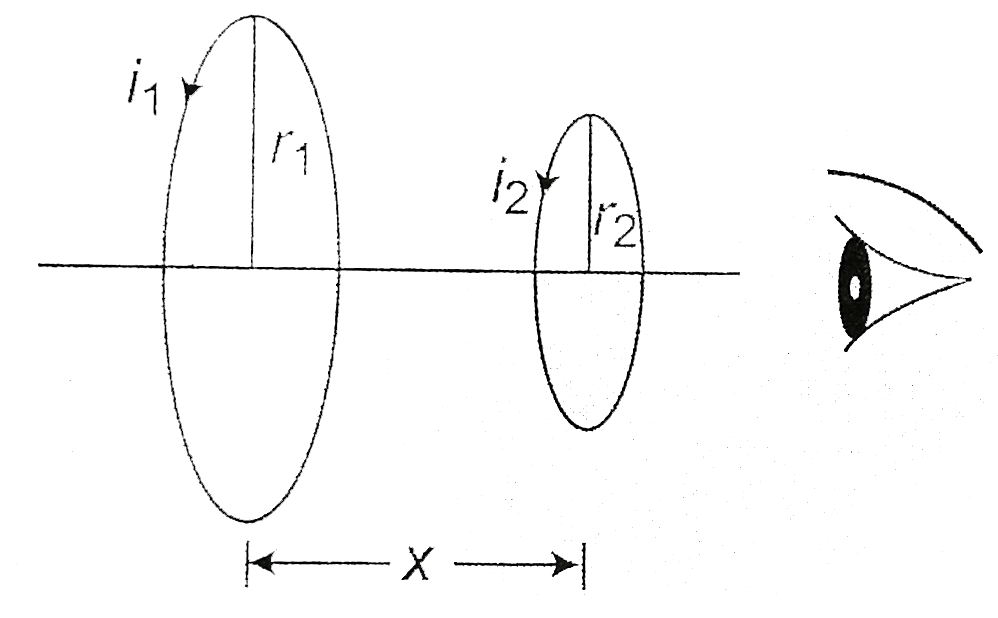
View SolutionTwo infinite long straight parallel wires A and B are separted by 0.1m distance and carry equal currents in opposite directions. A square loop of wire C of side 0.1m lies in the plane of A and B. The loop of wire C is kept parallel to both A and B at a distance of 0.1m from the nearest wire. Calculate the EMF induced in the loop C while the currents in A and B are increasing at the rate of 103A/s. Also indicate the direction of current in the loop C.
View Solution
Knowledge Check
Two coaxial circular loops of radius 0.5m and 5×10−2m are separated by a distance 0.5m and carry currents 2A and 1A respectively. The force between the loops due to mutual induction is
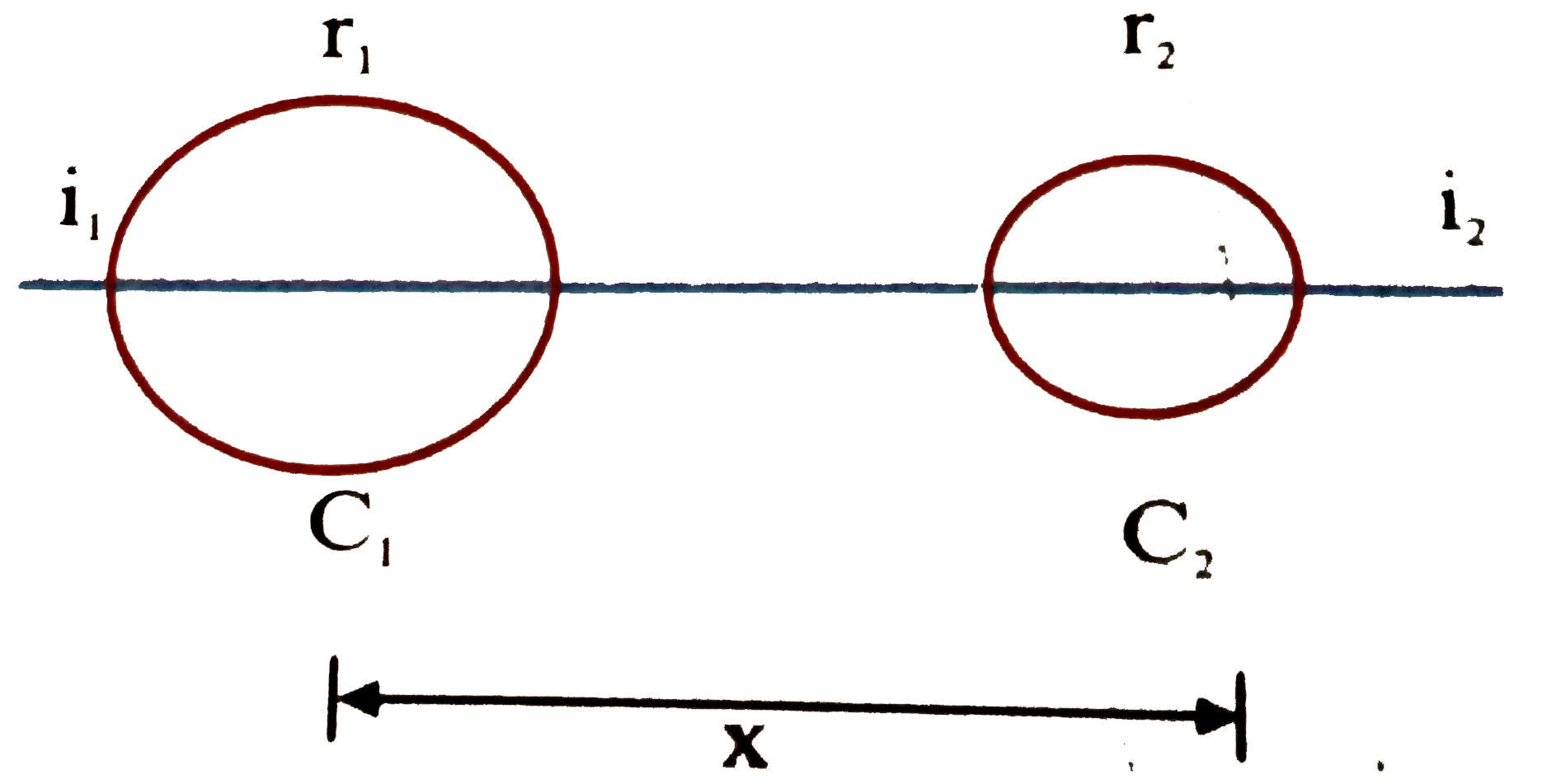 A2.09×10−8NB1.06×10−6NC4.18×10−8ND8.3×10−5N
A2.09×10−8NB1.06×10−6NC4.18×10−8ND8.3×10−5NA circular loop of radius 0.0157 m carriesa current of 2.0 A. The magnetic field at the centre of the loop is
A1.57×10−5Wb/m2B8.0×10−6Wb/m2C2.5×10−5Wb/m2D3.14×10−5Wb/m2There are two charges +1 μC and +5μC, separated by a distance of 0.2 m in air, the ratio of forces acting in them will be:
A1:5B5:1C1:1D1:25
Two circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
View SolutionTwo identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
View SolutionA parallel plate capacitor consits of two circular plates of radius R = 0.1 m. they are separated by a distance d = 0.5 mm. If electric field between the capacitor plates charges as
dEdt=5×1013Vm×s. Find displacement current between the plates.
View SolutionTwo circular loops of radii 0.05 and 0.09m, respectively, are put such that their axes coincide and their centers are 0.12m apart. A charge of 10−6C is spread uniformly on each loop. Find the potential difference between the centers of the loops.
View SolutionTwo identical rings PandQ of radius 0.1m are mounted coaxially at a distance 0.5m apart. The charges on the two rings are 2μCand4μC, respectively. The work done in transferring a charge of 5μC from the center of P to that of Q is.
View Solution
