Two poles of a horse-shoe magnet are separated by 0.1 m. Pole strength is 0.01 ampm. The magnetic field produced at a point midway between the poles will be
Zero
2×10−7T
2×10&T
8×10−7T
The correct Answer is:D
H=μ04πmd2
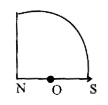
Field at O=2×μ04π×m(NO)2=2×10−7×.01(0.12)28×10−7T
Similar Questions
The distance between the poles of a horse shoe magnet is 0.1 m and its pole strength is 0.01 amp-m. The induction of magnetic field at a point midway between the poles will be

View SolutionTwo poles of a horse shoe magnet each of pole strength 2 Am are 8 cm apart. Find the magnetic field intensity at the midpoint of the line joining the poles.
View Solution
Knowledge Check
The distance between the poles of a horse shoe magnet is 0.1 m and its pole strength is 0.01 amp-m. The induction of magnetic field at a point midway between the poles will be
 A2×10−5TB4×10−6TC8×10−7TDZero
A2×10−5TB4×10−6TC8×10−7TDZeroThe pole strength of a horse shoe magnet is 90Am and distance between the poles is 6cm. The magnetic induction at mid point of the line joining the poles is,
A10−2TBzeroC2×10−2TD10−4TThe pole strength of a magnet is
Avector quantity with SI unit A mBscalar quantity with SI unit A/mCvector quantity with SI unit A/mDscalar quantity with SI unit A m
When a small piece of wire passes between the magnetic poles of a horse-shoe magnet in 0.1 sec, emf of 4×10–3 volt is induced in it. The magnetic flux between the poles is :
View SolutionThe pole piece of a horse shoe magnet are made cylindrical so that the deflection of the
View SolutionA bar magnet is 0.1 m long and its pole strength is 12 Am. Find the magnetic induction at a point on its axis at a distance of 0.2 m from its centre.
View SolutionTwo identical bar magnets of magnetic pole strength 10 Am and length 10 cm are placed 2 m apart such that their axes are perpendicular to each other. Calculate the resultant magnetic field at a point midway between the magnets.
View SolutionThe pole piece of a horse shoe magnet are made cylindrical so that the deflection of the
View Solution
