An electron in the ground state of hydrogen atom is revolving in a circular orbit of radius R. Ifm is the mass of the electron, e its charge, and h Planck's constant, the orbital magnetic dipole moment of the electron is
h2πmR
eh4π2R2m
eh4πm
zero
From the Bohr quantum condition, we have
mvR=nh2π
where v is the speed of the electron.
For ground state, n=1Sov=h2πmR
Current around the orbit is I=eT=e2πR/v=ev2πR=eh4π2R2m
Magnetic dipole moment is IA=I×πR2=eh4π2R2m×πR2=eh4πm
Similar Questions
An electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in the circular orbit of radius R as shown in figure.

Obtain an expression for the orbital magnetic dipole moment of the electron.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
View Solution
Knowledge Check
An electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
Aeh4πmBeh2πmCeh24πmDe2h4πmAn electron in the ground state of hydrogen atom is revolving in anticlockwise direction in circular orbit of radius R. The orbital magnetic dipole moment of the electron will be
Aeh4πmBeh2πmCeh24πmDe2h4πmAn electron in the ground state of hydrogen atom is revolving in anticlockwise direction in the circular orbit of radius R. The atom is placed in a uniform magnetic induction B such that the plane normal of electron orbit makes an angle 30∘ with B, as shown in figure. The torque experienced by electron will be
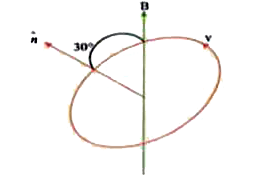 . AehB8πmBeh8πBmCeB8πmhDhB8πem
. AehB8πmBeh8πBmCeB8πmhDhB8πem
An electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.
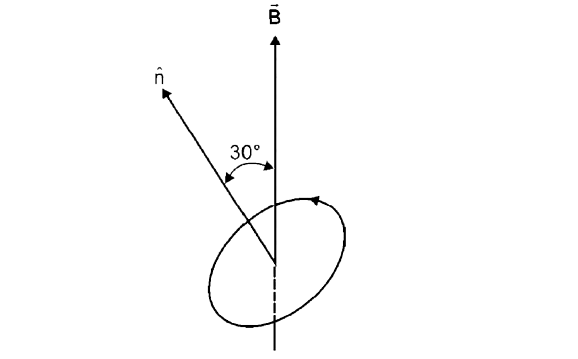
View SolutionAn electron in the ground state of hydrogen atom is revolving in anticlock-wise direction in a circular orbit of radius R.
(i) Obtain an experssion for the orbital magnetic dipole moment of the electron.
(ii) The atom is placed in a uniform magnetic induction →B such that the plane - normal of the electron - orbit makes an angle of 30∘ with the magnetic induction . Find the torque experienced by the orbiting electron.

View SolutionShow that the orbital magnetic dipole moment of a revolving electron isevr/2.
View SolutionAn electron in the ground state of hydrogen atom is revolving in anti-clockwise direction in a circular orbit of radius R.

(i) The expression for the orbital magnetic moment of the electrton is ehnπm. Find n □
(ii) The atom is placed in a uniform magnetic induction B such that the normal to the plane of electron’s orbit makes an angle of 30∘ with the magnetic induction. The torque experienced by the orbiting electron is ehBnπm. Find n □
View SolutionShow that the orbital magnetic dipole moment of a revolving electron isevr/2.
View Solution
