एक चल कुण्डली गैल्वेनोमीटर की कुण्डली में N फेरे हैं, क्षेत्रफल A है तथा k कमानी का ऐंठन नियतांक है।
यदि एकसमान रेडियल चुम्बकीय क्षेत्र B में धारा I के कारण कुण्डली में विचलन ϕ हो, तो-
ϕ=(NABk)l
ϕ=(kBNA)l
ϕ=(kABN)l
ϕ=(BNkA)l
The correct Answer is:A
जब इस कुण्डली से कोई विद्युत प्रवाहित की जाती है, तो इस पर एक बल-आघूर्ण कार्य करता है। इस बल-आघूर्ण τ का मान होता है
τ=NIAB
जहाँ, भौतिक राशियों के प्रतीकों के अपने सामान्य अर्थ हैं। चूंकि डिजाइन के अनुसार, चुम्बकीय क्षेत्र रेडियल है, हमने बल-आघूर्ण के लिए दिए गए उपरोक्त व्यंजन में sinθ=1 लिया है। यह चुम्बकीय बल-आघूर्ण NIAB कुण्डली में घूर्णन की प्रवृत्ति उत्पन्न करता है, जिसके फलस्वरूप कुण्डली अपने अक्ष पर घूर्णन करती है। कुण्डली से जुड़ी कमानी SP में कुण्डली के घूर्णन के विरोध में बल-आघूर्ण kϕ उत्पन्न हो जाता है, जो कुण्डली के बल-आघूर्ण NIAB को सन्तुलित करता है, फलस्वरूप कुण्डली में ϕ कोण का स्थायी कोणीय विक्षेप आ जाता है। साम्यावस्था में,
kϕ=NIAB
जहाँ, k कमानी का ऐंठन (torsional) नियतांक है, अर्थात् प्रति एकांक ऐंठन प्रत्यानयन (torsional) बल-आघूर्ण है। विक्षेप ϕ का पाठ्यांक कमानी के साथ जुड़े संकेतक द्वारा पैमाने पर लिया जा सकता है। उपरोक्त व्यंजक के अनुसार ϕ का मान है
ϕ=(NABk)I
Topper's Solved these Questions
- गतिमान आवेश और चुम्बकत्वBOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश और चुम्बकत्वEXERCISE - Special Format वाले Objective प्रश्न (I. कथन-कारण (Assertion-Reason) )
5 Videos
- गतिमान आवेश और चुम्बकत्वBOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश और चुम्बकत्वEXERCISE - Special Format वाले Objective प्रश्न (II. कथन प्रकार I (Statement Type I) )
5 Videos
- गतिमान आवेश और चुम्बकत्वBOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश और चुम्बकत्वEXERCISE - NCERT पर based Objective प्रश्न ( टॉपिक 4 धारा लूप तथा चुम्बकीय द्विध्रुव पर बल आघूर्ण (Torque on Current Loop and Magnetic Dipole) )
19 Videos
- गतिमान आवेश एवं चुम्बकीय क्षेत्र BOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश एवं चुम्बकीय क्षेत्र EXERCISE - MCQs
54 Videos
- गतिमान आवेश तथा चुम्बकत्व BOOK - NEET PREVIOUS YEARCHAPTER - गतिमान आवेश तथा चुम्बकत्व EXERCISE - बहुविकल्पीय प्रश्न
71 Videos
Similar Questions
निर्देश : निम्न प्रश्नों में, 'कथन के वक्तव्य के बाद कारण के वक्तव्य को दिया गया है। जिसके आधार पर सही विकल्प पर निशान लगाइए।
कथन साइक्लोट्रॉन एक ऐसा यन्त्र है, जो धनात्मक आयनों को त्वरित करने के लिए प्रयुक्त होता है।
कारण साइक्लोट्रॉन की आवृत्ति वेग पर निर्भर करती है।
View Solutionनिर्देश : निम्न प्रश्नों में कथन I के वक्तव्य के बाद कथन II के वक्तव्य को दिया गया है। जिसके आधार पर सही विकल्प पर निशान लगाइए।
कथन I जब एक आवेशित कण लम्बवत् चुम्बकीय क्षेत्र में गतिमान होता है, तो उसकी चाल नियत रहती है।
कथन II इस आवेशित कण पर लगा चुम्बकीय बल,
F=q(v×B)
View Solution10 सेमी तथा 5 सेमी भुजाओं के एक आयताकार लूप से एक विद्युत धारा I=12 ऐम्पियर, प्रवाहित हो रही है। इस लूप को आरेख में दर्शाए गए अनुसार विभिन्न अभिविन्यासों (स्थितियों) में रखा गया है।
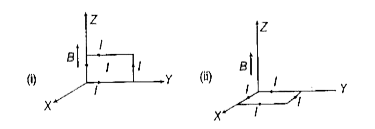
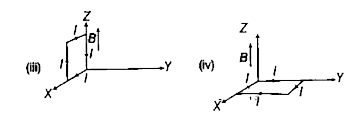
यदि वहाँ 0.3 टेस्ला तीव्रता का कोई एकसमान चुम्बकीय क्षेत्र धनात्मक Z−दिशा में विद्यमान है, तो दर्शाए गए किस अभिविन्यार में, यह लूप स्थायी सन्तुलन तथा अस्थायी सन्तुलन में होगा?
View Solutionकिसी चल कुण्डली गैल्वेमीटर की धारा सुग्रहिता 5div/mA और वोल्टता सुग्राहिता ( प्रयुक्त इकाई वोल्टता से उत्पन्न कोणीय विक्षेप ) 20div/V है। इस गैल्वेमीटर का प्रतिरोध है
View Solutionएक धारा प्रवाहित कुण्डली एक समान चुम्बकीय क्षेत्र में रखी गयी है। कुण्डली घूमेगा ताकि उसका समतल
View Solutionउचित संबंध जोड़िए-
स्तम्भ 'अ'स्तम्भ 'ब'1.डायनेमो की खोज(a)लेंज का नियम2.भँवर धारा(b)एक कुण्डली3.स्वप्रेरण(c)फैराडे4.अन्योन्य प्रेरण(d)फोको धारा5.प्रेरित धारा की दिशा(e)दो कुण्डली।
View Solutionएक फूलों की क्यारी, जो एक वृत्त के त्रिज्याखण्ड के रूप में है, की घेराबंदी करने के लिए 20 मीटर तार उपलब्द है। तो फूलों की क्यारी का अधिकतम क्षेत्रफल (वेग मी) में है
View Solutionचुम्बकीय क्षेत्र तथा चुम्बकीय क्षेत्र की तीव्रता | एक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता
View Solutionचुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionचुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionएक अकेले चुम्बकीय ध्रुव के कारण चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण अक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता | चुम्बकीय द्विध्रुव के कारण निरक्षीय स्थिति में चुम्बकीय क्षेत्र की तीव्रता
View Solutionएकसमान चुम्बकीय क्षेत्र में चुम्बकीय द्विध्रुव पर बल आधूर्ण तथा कार्य | पृथ्वी का चुम्बकीय क्षेत्र तथा अवयव | V,H तथा I में सम्बन्ध
View Solutionपरिनालिका तथा कुण्डली
View Solutionएकसमान चुम्बकीय क्षेत्र में आवेश की गति
View Solutionएकसमान चुम्बकीय क्षेत्र में गतिमान आवेश (2)
View Solutionटोरोइड के कारण चुम्बकीय क्षेत्र | एक समान चुम्बकीय क्षेत्र में गतिमान आवेश पर बल
View Solution
