An alternating voltage E=E0sinωt is applied to a circuit containing a resistor R connected in series with a black box. The current in the circuit is found to be I=I0sin(ωt+π4).
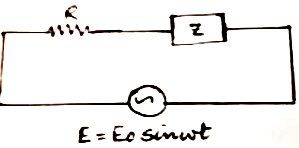
An alternating voltage E=E0 sin omegat is applied to a circuit containing a resistor R connected in series with a black box. The current in the circuit is found to be I = I0 sin(omegat+pi/4). State whether the element in the black box is a capacitor or indutor.
State whether the element in the black box is a capacitor or indutor.Solution in Punjabi

Video Solution
Doubtnut Promotions Banner
|
Answer

Step by step video & image solution for An alternating voltage E=E_0 sin omegat is applied to a circuit containing a resistor R connected in series with a black box. The current in the circuit is found to be I = I_0 sin(omegat+pi/4).State whether the element in the black box is a capacitor or indutor. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023