The self inductance of a straight conductor is zero.
To determine whether the self-inductance of a straight conductor is zero, we can analyze the concept of self-inductance step by step.
1. Understanding Self-Inductance:
Self-inductance is a property of a coil or conductor that opposes changes in the current flowing through it. It is defined mathematically as the ratio of the induced electromotive force (EMF) in the coil to the rate of change of current through it.
2. Formula for Self-Inductance:
The self-inductance (L) of a coil is given by the formula:
L=NΦI
where N is the number of turns in the coil, Φ is the magnetic flux linked with each turn, and I is the current flowing through the coil.
3. Characteristics of a Straight Conductor:
A straight conductor does not have multiple turns like a coil. It is essentially a single wire through which current flows. Therefore, in the case of a straight conductor, the number of turns N is equal to 0.
4. Calculation of Self-Inductance for a Straight Conductor:
Since self-inductance depends on the number of turns, if N=0, then:
L=0⋅ΦI=0
This indicates that the self-inductance L of a straight conductor is indeed zero.
5. Conclusion:
Therefore, we conclude that the self-inductance of a straight conductor is zero because it lacks the necessary turns to create a magnetic field that can induce an EMF opposing the change in current.
Self-inductance is a property of a coil or conductor that opposes changes in the current flowing through it. It is defined mathematically as the ratio of the induced electromotive force (EMF) in the coil to the rate of change of current through it.
The self-inductance (L) of a coil is given by the formula:
L=NΦI
where N is the number of turns in the coil, Φ is the magnetic flux linked with each turn, and I is the current flowing through the coil.
A straight conductor does not have multiple turns like a coil. It is essentially a single wire through which current flows. Therefore, in the case of a straight conductor, the number of turns N is equal to 0.
Since self-inductance depends on the number of turns, if N=0, then:
L=0⋅ΦI=0
This indicates that the self-inductance L of a straight conductor is indeed zero.
Therefore, we conclude that the self-inductance of a straight conductor is zero because it lacks the necessary turns to create a magnetic field that can induce an EMF opposing the change in current.
Topper's Solved these Questions
- BOOK - MBD -HARYANA BOARDCHAPTER - E.M.I. and A.C.EXERCISE - Exercise10videos
E.M.I. and A.C.
- BOOK - MBD -HARYANA BOARDCHAPTER - DUAL NATURE OF MATTER AND RADIATIONSEXERCISE - OBJECTIVE TYPE QUESTIONS17videos
DUAL NATURE OF MATTER AND RADIATIONS
- BOOK - MBD -HARYANA BOARDCHAPTER - Electromagnetic WavesEXERCISE - Example7videos
Electromagnetic Waves
Similar Questions
Knowledge Check
- Question 1 - Select One
The self inductance of a toroid is :-
Aμ0N2r22RmBμ0N2πr2RmCμ0N2r2RmDμ0N2rπrm - Question 2 - Select One
The self inductance of a coil is a measure of
Aelectrical inertiaBelectrical frictionCinduced emf and the magnetic fluxDinduced current - Question 3 - Select One
Unit of self inductance is
ANewton-secondCoulomb×AmpereBJoule/Coulomb×SecondAmpereCVolt×metreCoulombDNewton×metreAmpere
Self Induction
View SolutionSelf inductance || L-R Circuit
View SolutionDistinguish between self induciton and Self induction. Give two factors on which self inductance of an air cored coil depends ?
View SolutionThe unit of self inductance of a coil is
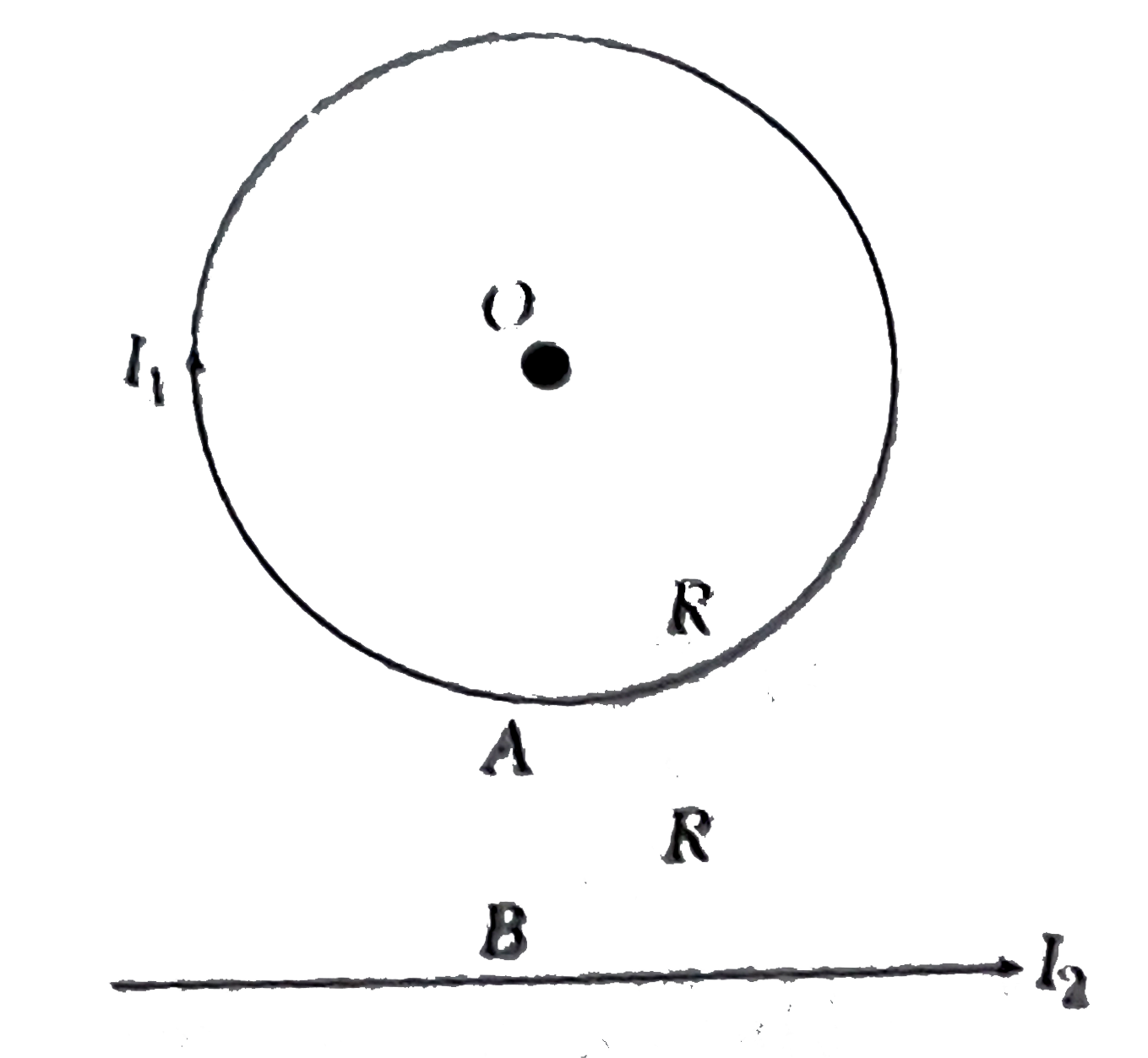
View SolutionIn the diagram I1,I2 are the strength of the currents in the loop and straight conductors respectively OA=AB=R. the net magnetic field at the centre O is zero . Then the ratio of the currents in the loop and the straight conductor is
 View Solution
View Solution

