Find the range of f(x)=x2+34x−71x2+2x−7Solution in Gujrati
Video Solution
Text Solution
Let x2+34x−71x2+2x−7=y
⇒x2(y−1)+(2y−34)x+71−7y=0
For real values of x discriminant ≥0
∴(2y−34)2−4(y−1)(71−7y)≥0
⇒8y2−112y+360≥0
⇒y2−14h+45≥0
⇒(y−9)(y−5)≥0
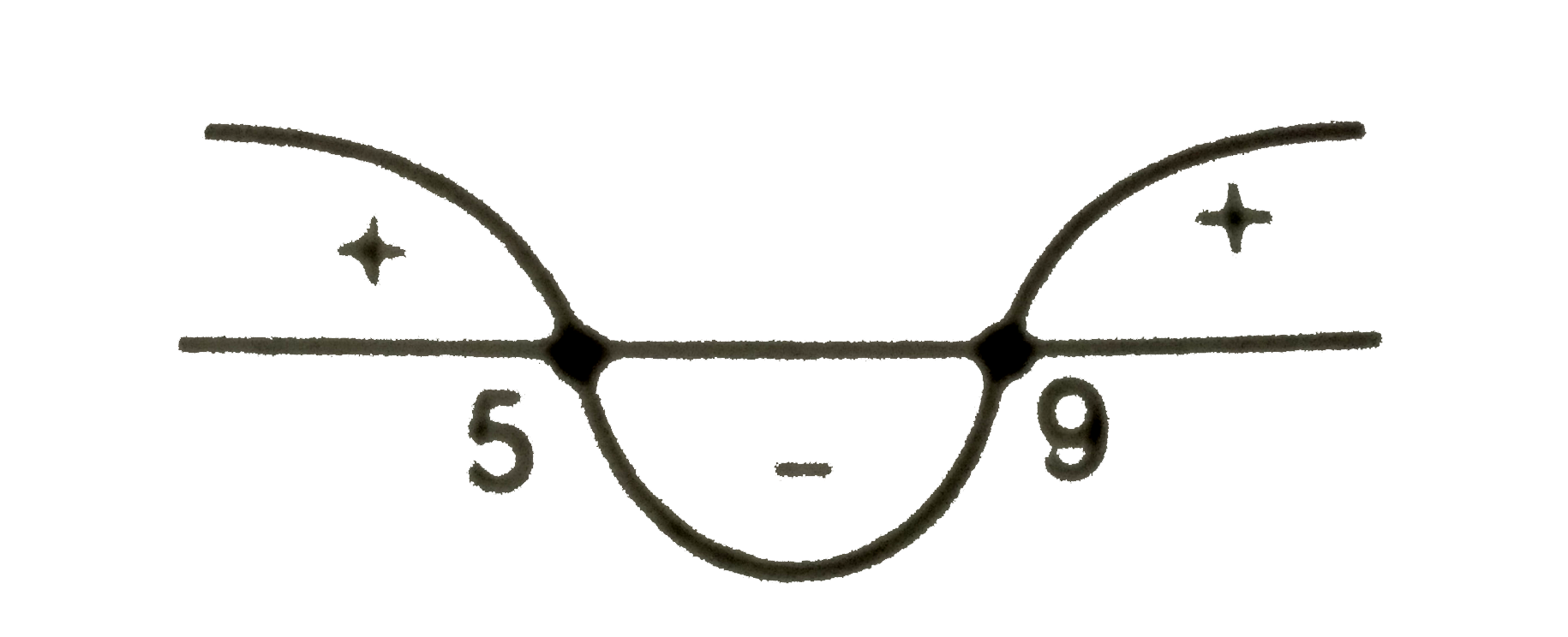
⇒yε(−∞,5]∪[9,∞)
Hence y can never lie betwene 5 and 9.
|
Similar Questions
Range of f(x)=x2−xx2+2x is …….
View SolutionFind the range of f(x)=x2+34x−71x3+2x−7
View SolutionFind the range of f(x)=2x2−1
View SolutionIf x is real then the values of x2+34x−71x2+2x−7 does not lie in the interval
View SolutionFind the range of
(a) f(x)=x2+2x+4
(b) f(x)=1+x−x2
View SolutionThe range of f(x)=2+2x+x2 is
View SolutionThe range of f(x)=2+2x−x2 is :
View SolutionFind the range of the expression x2+34x−71x2+2x−7, if x is a real.
View Solution
