Question

Solve the equation ${\displaystyle |x-1|+|7-x|+2|x-2|=4}$

Explanation

Here critical points are 1,2,7 using the method of intervals, we find intervals when the expression `x-1,7-x` and `x-2` are of constant signs.
i.e. `xlt1, 1ltx lt 2, 2 lt x lt 7,x gt7`

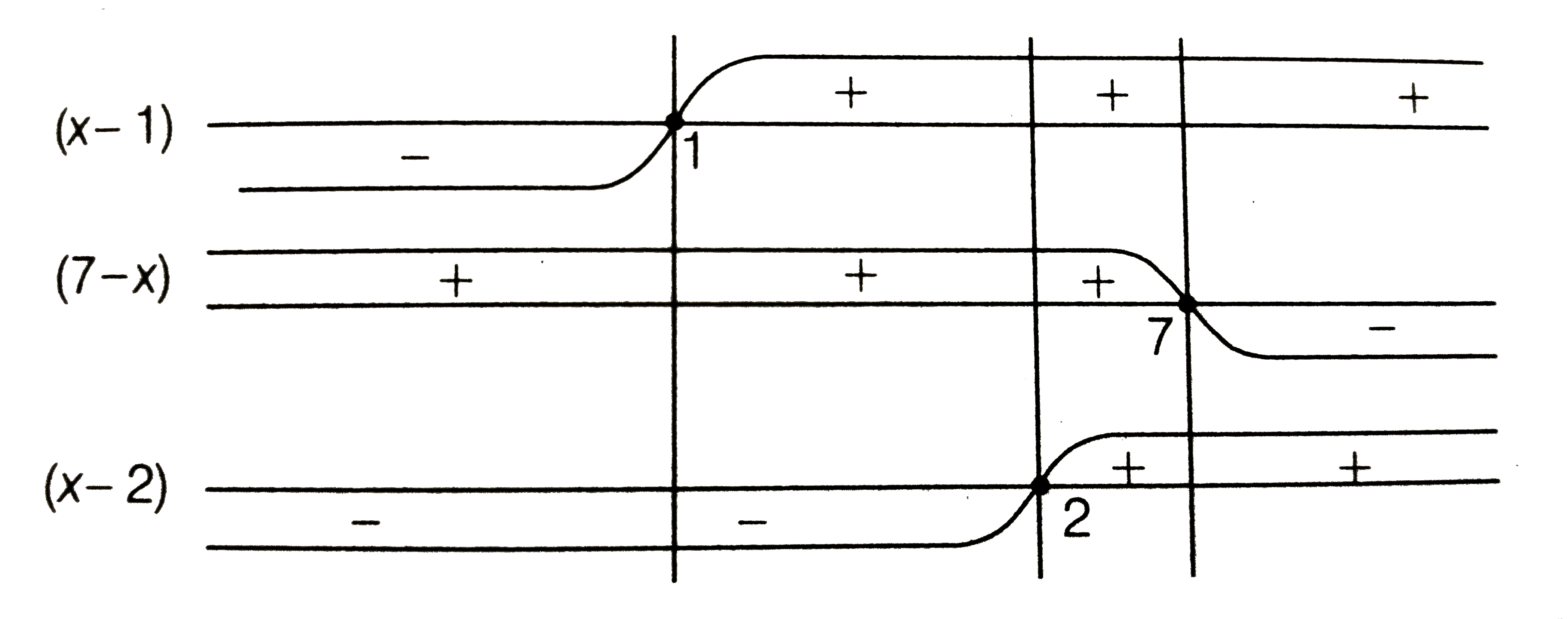
Thus, the given equation is equivalent to the collection of four systems,
`[({(xlt1),(-(x-1)+(7-x)-2(x-2)=4):}),({(1lexlt2),((x-1)+(7-x)-2(x-2)=4):}),({(2lexlt7),((x-1)+(7-x)+2(x-2)=4):}),({(xge7),((x-1)-(7-x)+2(x-2)=4):}):} `implies[({(xlt1),(x=2):}),({(1lexlt2),(x=3):}),({(2lexlt7),(x=1):}),({(xge7),(x=4):}):}`
From the collection of four systems, the given equation has no solution.