Solve √x+3−4√x−1+√x+8−6√x−1=1Solution in Gujrati
Video Solution
Text Solution
Let √(x−1)=t
We have x=t2+1,t≥0
The given equation reduce in the form
√(t2+4−4t)+√(t2+9−6t)=1
⇒|t−2|+|t−3|=1
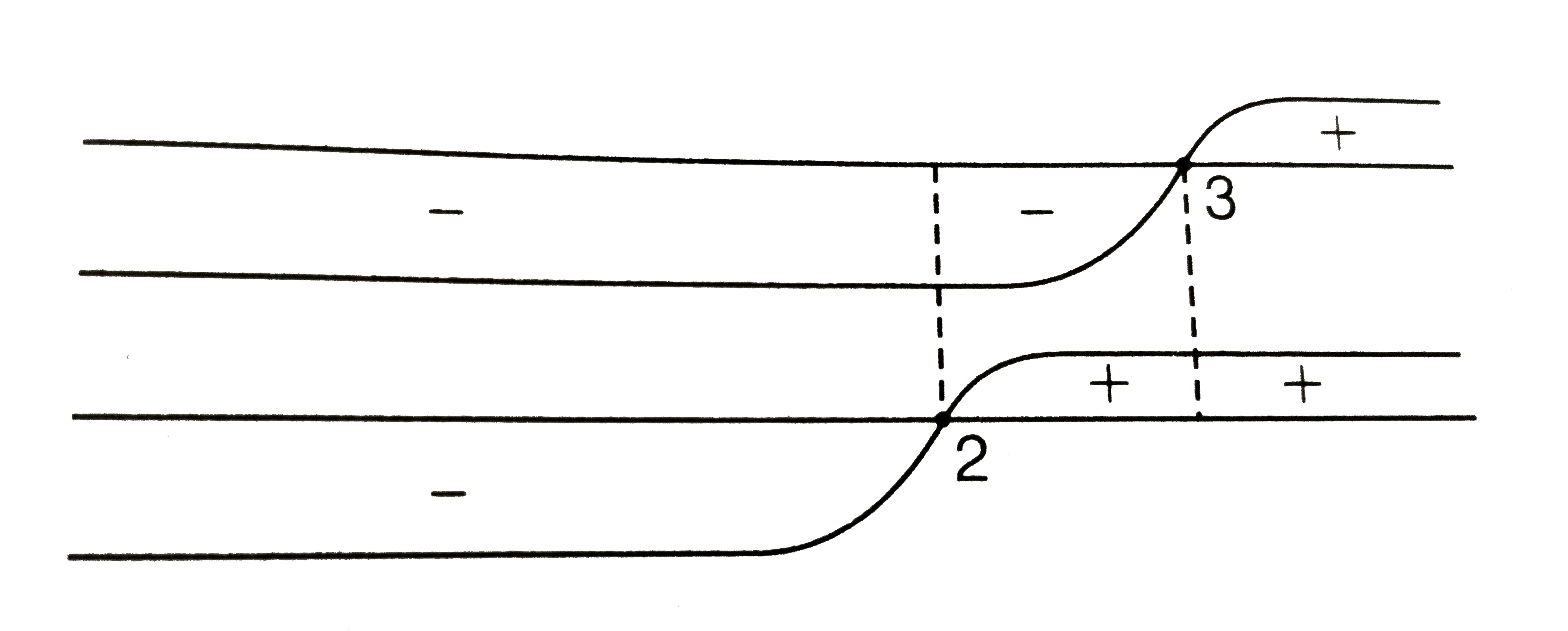
∴2≤t≤3
⇒4≤t2≤9
⇒4≤x−1≤9
⇒5≤x≤10
∴ Solution of the original equation is xε[5,10]
|
Similar Questions
Solve √x+1+√x−1√x+1−√x−1
View SolutionSolve :√1+x−√1−x√1+x+√1−x
View SolutionSolve foe x∈R √x+8+6√x−1−√x+3+4√x−1=1.
View Solutionthe equation log_(3) (sqrt(x)+|sqrt(x)-1|) =log_(9) (4sqrt(x)-3+4|sqrt(x)-1|) Solve for x
View Solutionवास्तविक संख्या पद्धति में, समीकरण
√x+3−4√x−1+√x+8−6√x−1=1 के लिए
View Solutionनिम्नलिखित सामीकरणों को हल करें
√1+x+√1−x√1+x−√1−x=ab
View SolutionIf f(x)=√x+3−4√x−1+√x+8−6√(x−1),then|o|lutevalueoff^(')(x) at x = 1.5 is
View SolutionIf x=sqrt(7+4sqrt(3)), prove that x+1//x=4
View Solution
