If both roots of the equation lie between then a lies in the intervalSolution in Gujrati
The correct Answer is:B
Let
Now four cases arise:
Case I
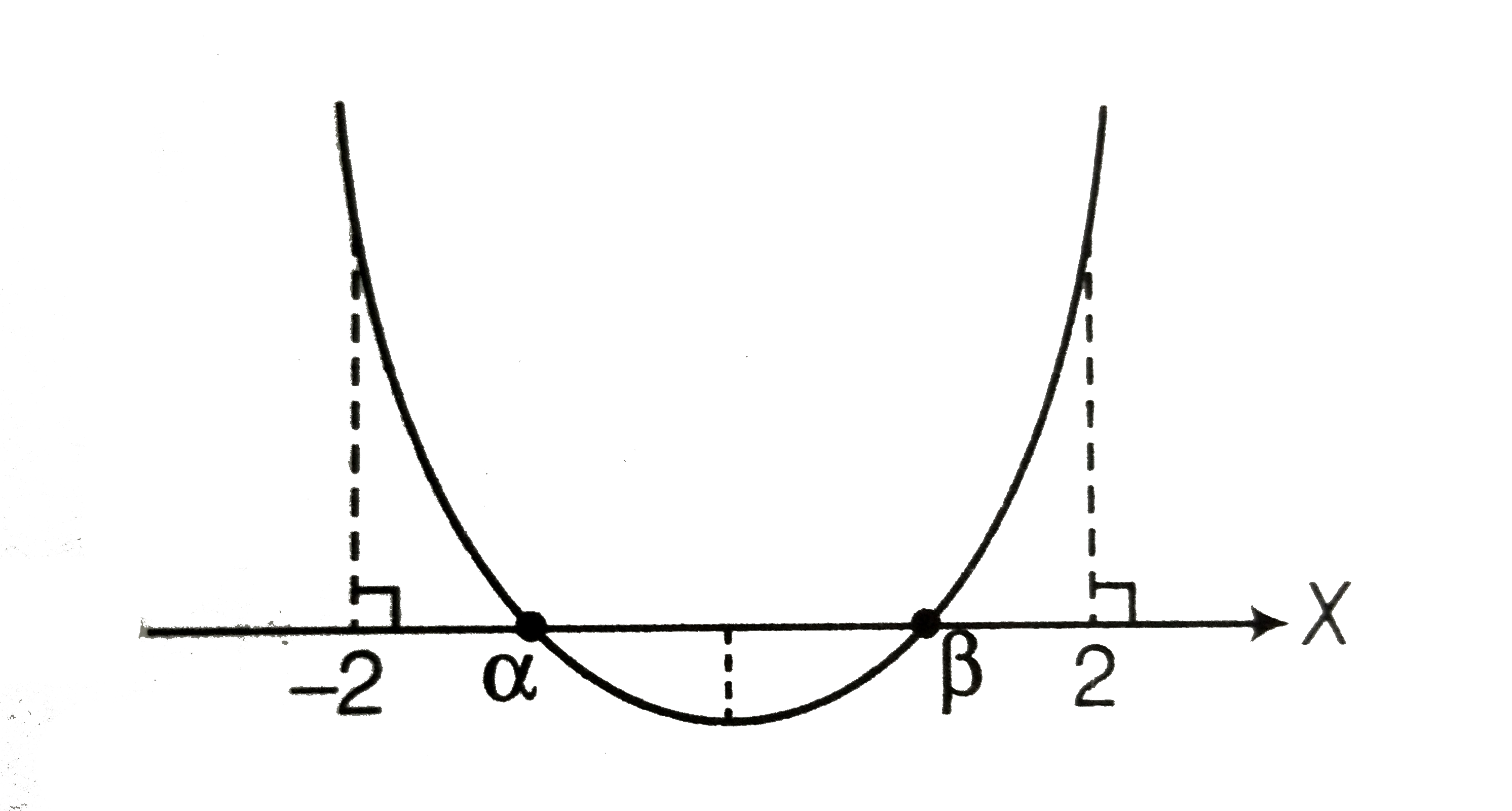
ltbr>gt
Case II
Case III
Case IV coordinate of vertex
Hence
Similar Questions
The interval in which the real number a lies so that the roots of x2−2ax+a2=0 lies between - 2 and 4 is
View SolutionThe values of a for which both the roots of the equation (1−a2)x2+2ax−1=0 lie between 0 and 1 are given by
View SolutionThe value of a for which both the roots of the equation (1−a2)x2+2ax−1=0 lie between 0 and 1, will always be greater than
View SolutionIf the roots of x2−2kx+k2−1=0 lie between -2 and 4 then the interval in which k lies, is
View SolutionIf both the roots of the quadratic equation x2−mx+4=0 are real and distinct and they lie in the interval [1, 5], then m lies in the interval
View SolutionIf both roots of the equation x2−2ax+a2−1=0 lie between -3 and 4 ,then [a] is/are , where [ ] represents the greatest ineger function
View SolutionFind all the values of 'a' for which both the roots of the equation (a−2)x2−2ax+a=0 lies in the interval (−2,1).
View SolutionThe value of a for which both the roots of the equation (1−a2)x2+2ax−1=0 lie between 0 and 1, will always be greater than
View Solution
