Find all values of a for which the inequation $4^{x^{2}} + 2 (a + 1) 2^{x^{2}} + 4 a^{2} - 3 > 0$ is satisfied for any $x$ .Solution in Gujrati

Video Solution

Text Solution

Verified by Experts

The correct Answer is: $a ε (- \infty, - 1) \cup (\frac{\sqrt{3}}{2}, \infty)$

We have $4^{x^{2}} + 2 (2 a + 1) 2^{x^{2}} + 4 a^{2} - 3 > 0$ ….i
Putting $t = 2^{x^{2}}$ in the Eq. (i) we get
$t^{2} + 2 (2 a + 1) t + 4 a^{2} - 3 > 0$
Let $f (t) = t^{2} + 2 (2 a + 1) t + 4 a^{2} - 3 [∵ t > 0, ∴ 2^{x^{2}} > 0]$
$∵ f (t) > 0$

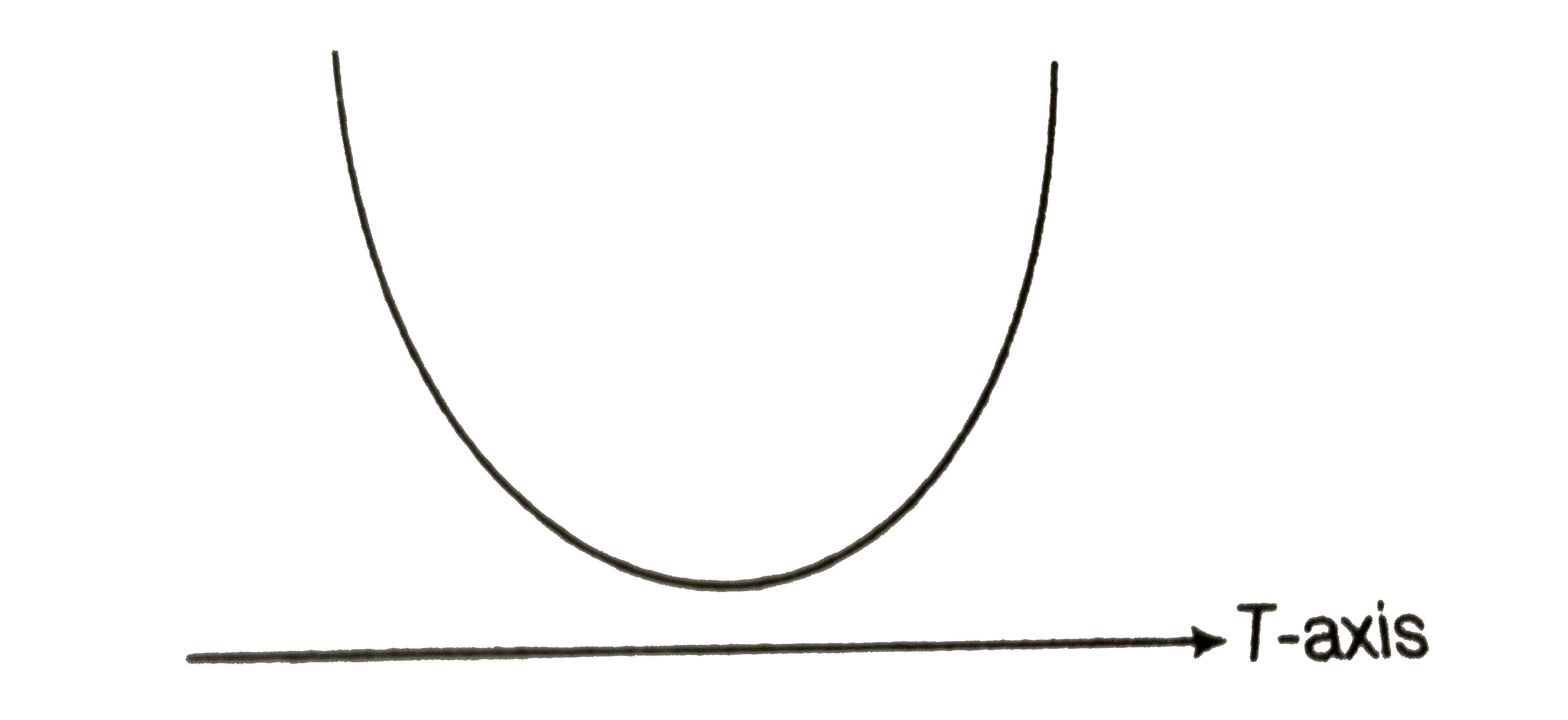
Case Sum of the roots $> 0$
$- 2 \frac{(2 a + 1)}{1} > 0$
$∴ a ε (- \infty, - \frac{1}{2})$
Case II Product of the roots $> 0$
$\Rightarrow \frac{4 a^{2} - 3}{1} > 0$
or $a^{2} > \frac{3}{4}$
or $a ε (- \infty, - \frac{\sqrt{3}}{2}) \cup (\frac{\sqrt{3}}{2}, \infty)$
Case III $D < 0$
$\Rightarrow 4 {(2 a + 1)}^{2} - 4.1 . (4 a^{2} - 3) < 0$
$\Rightarrow 4 a + 4 < 0$
$∴ a < - 1$
or $a ε (- \infty, - 1)$
Combining all cases we get
$a ε (- \infty, - 1) \cup (\frac{\sqrt{3}}{2}, \infty)$

|

Updated on:21/07/2023

Class 12 MATHS QUADRATIC EQUATIONS

Similar Questions

Recommended Questions

Home
Ask Doubt
Profile