If α,β are the roots of the equation x2−2x−a2+1=0 and γ,δ are the roots of the equation
x2−2(a+1)x+a(a−1)=0 such that α,βεn(γ,δ) find the value of a.Solution in Gujrati
The correct Answer is:aε(−14,1)
Since the given equation is
x2−2x−a2+1=0
⇒(x−1)2=a2
∴x−1≠a or x=1±a
∴α=1+a and β=1−a
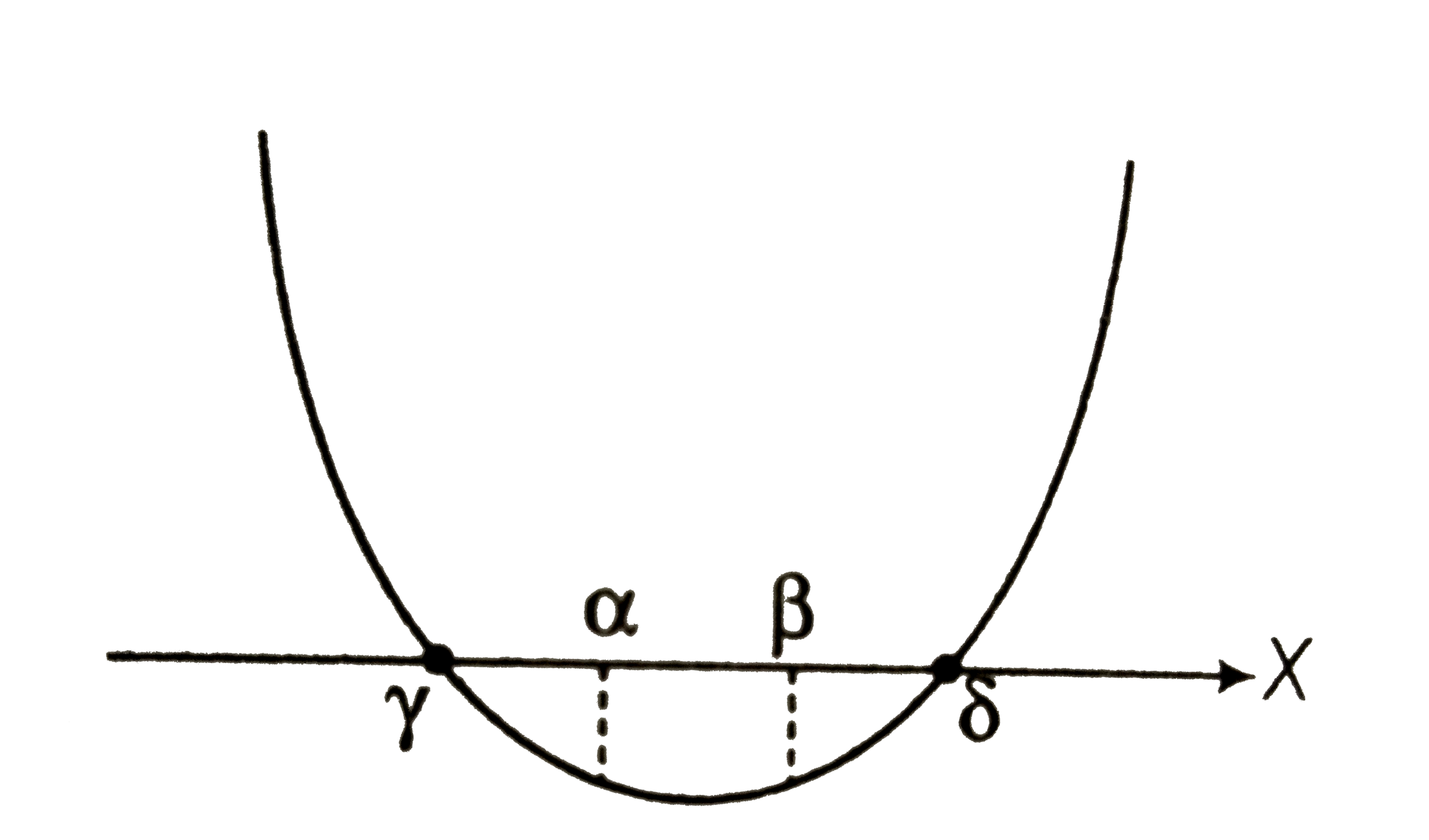
Let f(x)=x2−2(a+1)x+a(a−1) thus the following conditiions hold good:
Consider the followign cases:
Case I D>0
⇒4(a+1)2−4a(a−1)>0
⇒3a+1>0
∴a>−13
Case IIf(α)<0
⇒f(1+a)<0
⇒(1+a)2−2(1+a(1+a)+a(a−1)<0
⇒−(1+a)2+a(a−1)<0
⇒−3a−1<0
⇒a>−13
Case II f(s)=0
⇒f(1−a)<0
⇒(1−a)2−2(a+1)(1−a)+a(a−1)<0
⇒(4a+1)(a−1)<0
∴−14<a<1
Combining all cases we get
aε(−14,1)
Similar Questions
यदि α और β समीकरण x2+px−q=0 के तथा γ,δ समीकरण x2+px+r=0 के मूल हैं, तो सिद्ध कीजिए की, (α−γ)(α−δ)=(β−γ)(β−δ)=q+r
View SolutionIf α,β,γandδ are the roots of the equation x4−bx−3=0, then an equation whose roots are α+β+γδ2,α+β+δγ2,α+δ+γβ2,andδ+β+γα2, is:
View SolutionIf α,β are the roots of x2+px+1=0 and γ,δ are the roots of x2+qx+1=0 then (α−γ)(β−γ)(α+δ)(β+δ)=
View SolutionIf αandβ are the roots of the equation x2+px+1=0,gamam,δ are the roots of (x2+qx+1=0 , then , find (α−γ)(β−γ)(α+δ)(β+δ)
View SolutionIf αandβ are the roots of x2+qx+1=0 and γ,δ the roots of x2+qx+1=0, then the value of
(α−γ)(β−γ)(a+δ)β+δ) is :
View SolutionIf α,β be the roots of x2+x+2=0 and γ,δ be the roots of x2+3x+4=0 then (α+γ)(α+δ)(β+γ)(β+δ)=
View SolutionIf α,β,γandδ are the roots of the equation x4−bx−3=0, then an equation whose roots are α+β+γδ2,α+β+δγ2,α+δ+γβ2,andδ+β+γα2, is:
View SolutionIf α,β be the roots of x2+x+2=0 and γ,δ be the roots of x2+3x+4=0, then (α+γ)(α+δ)(β+γ)(β+δ) is equal to
View Solution
