Prove that (n!) is divisible by (n!)n−1!Solution in Gujrati
Video Solution
Text Solution
First we show that the product of p consecutive positive integers is divisible by p!. Let the p consecutive integers be m,m+1,m+2, . . ,m+p-1. then,
m(m+1)(m+2)..(m+p−1)=(m+p−1)!(m−1)
=p!(m+p−1)!(m−1)!p!
=p!.m+p−1Cp
Since, .m+p−1Cp is an integer
∴.m+p−1Cp=m(m+1)(m+2)...(m+p−1)p!
Now, (n!)! is the product of the positive integers from 1 to n!. we write the integers from 1 to n! is (n-1)! rows as follows:
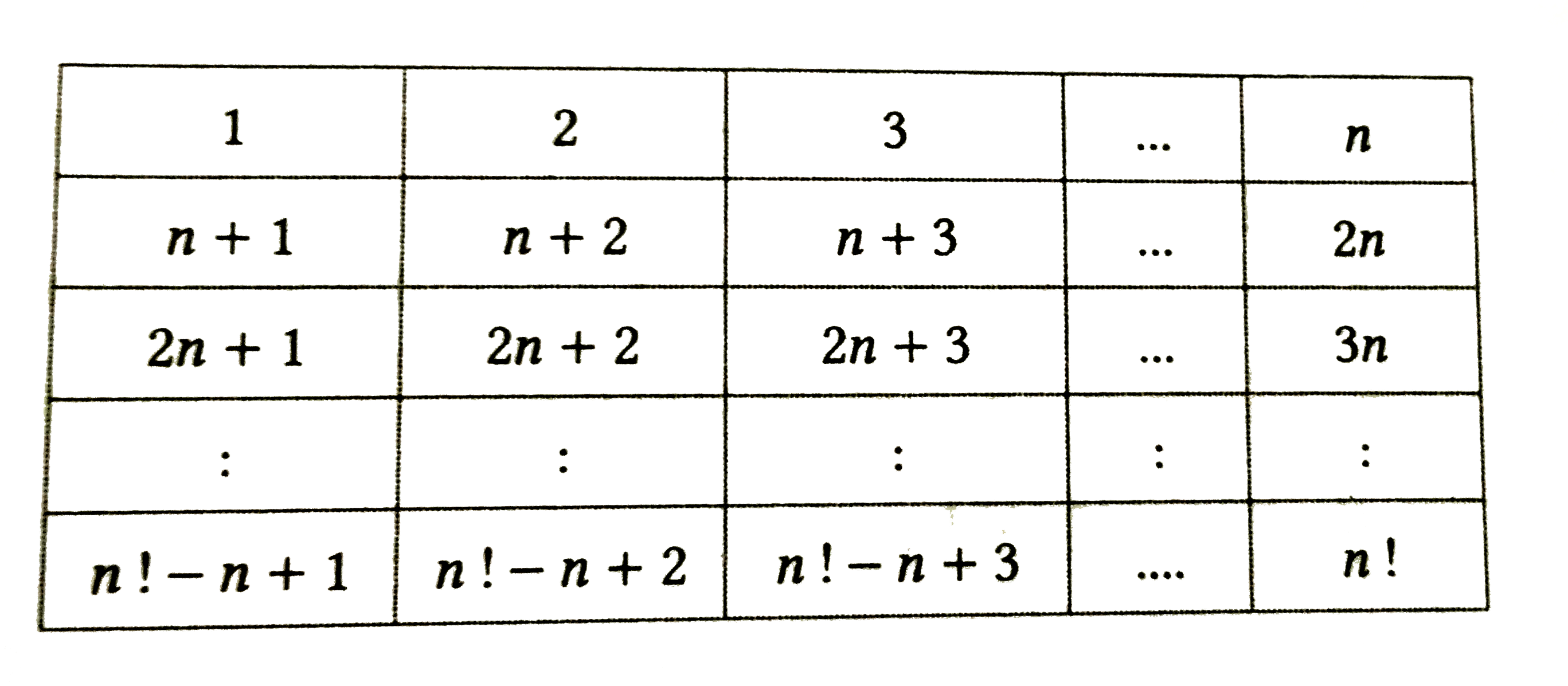 ltBrgt Each of these (n-1)! rows contains n consecutive positive integers. the products of the conescutive integers in each row is divisible by n!. thus, the product of all the integers from 1 to n! is divisible by (n1)(n−1)!.
ltBrgt Each of these (n-1)! rows contains n consecutive positive integers. the products of the conescutive integers in each row is divisible by n!. thus, the product of all the integers from 1 to n! is divisible by (n1)(n−1)!.
|
Similar Questions
prove that 4n−1 is divisible by 3, for each natural number n.
View SolutionProve that (n!+1) is not divisible by any natural number between 2 and n
View SolutionProve that (n!+1) is not divisible by any natural number between 2 and n
View SolutionProve that ∀n∈N
33n−26n−1 is divisible by 676.
View SolutionProve that ∀n∈N
54n+52n−1 is divisible by 676.
View SolutionFor n∈N prove that 5n+2.3n−1+1 is divisible by 8.
View SolutionProve by the principle of mathematical induction that for all n in N.(102n−1+1) is divisible by 11 for all n∈N.
View SolutionProve that (mn)! Is divisible by (n!)^(m) " and" (m!)^(n)
View Solution
