Prove the following by the principle of mathematical induction: 11n+2+122n+1 is divisible 133 for all n∈N.Solution in Gujrati
Let P(n)=11n+2+122n+1
Step I For n=1,
P(1)=111+2+122×1+1=113+123
=(11+12)(112−11×12+122)
=23×13 , which is divisible by 133.
Therefore , the result is true for n=1.
Step II Assume that the result is true for n=k, then
P(k)=11k+2+122k+1 is divisible by 133.
⇒P(k)=133r, where r is an integer .
Step III For n=k+1.
∴P(k+1)=11(k+1)+2+122(k+1)+1=11k+3+122k+3
=11(k+1)+1.11+122k+1.122
=11.11k+2+144.122k+1
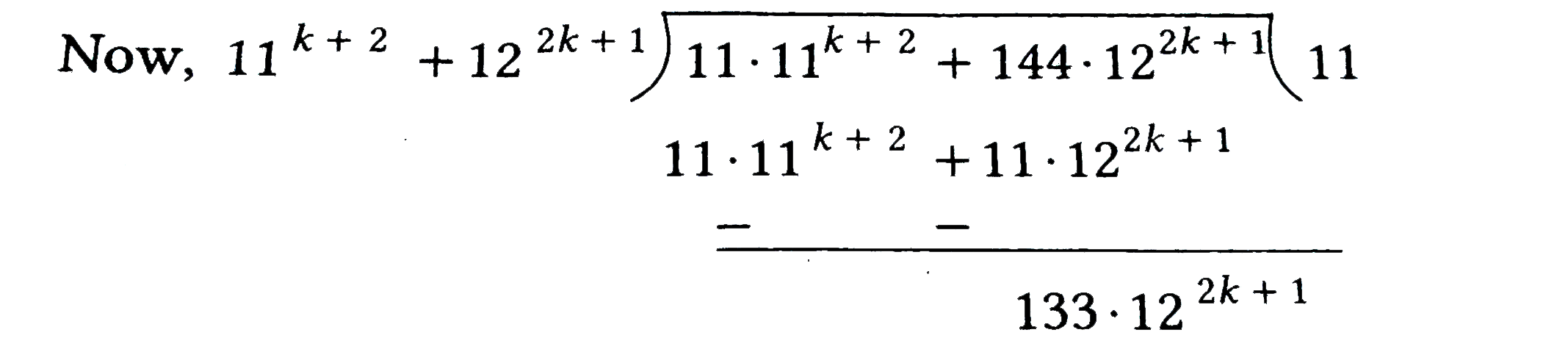
∴11.11(k+2)+144.122k+1=11(11k+2+122k+1)+133.122k+1
i.e., P(k+1)=11P(k)+133.122k+1
But we know that , P(k) is divsible by 133. Also , 133.122k+1 is divisible by 133.
Hence , P(k+1) is divisible by 133. This shows that , the result is true for n=k+1.
Hence , by the principle of mathematical induction , the result is true for all . n∈N.
Similar Questions
Prove the following by the principle of mathematical induction: 52n−1 is divisible by 24 for all n∈N.
View SolutionProve the following by the principle of mathematical induction: 32n+7 is divisible by 8 for all n∈N.
View SolutionProve the following by the principle of mathematical induction: 32n+2−8n−9 is divisible 8 for all n∈N.
View SolutionProve the following by the principle of mathematical induction: 72n+23n−3.3n−1 is divisible 25 for all n∈N.
View SolutionProve the following by using the principle of mathematical induction for all n∈N
102n−1+1 is divisible by 11.
View SolutionProve the following by using the principle of mathematical induction for all n∈N
11n+2+122n+1 is divisible by 133.
View SolutionProve the following by using the principle of mathematical induction for all n∈N :- 102n−1+1 is divisible by 11.
View SolutionProve by the principle of mathematical induction that for all n in N.(102n−1+1) is divisible by 11 for all n∈N.
View Solution
