Let α,β,γ be distinct real numbers. The points with position vectors αˆi+βˆj+γˆk,βˆi+γˆj+αˆk,γˆi+αˆj+βˆk Solution in Gujrati
are collinera
form an equilateral triangle
form a scalene triangle
form a right angled triangle
Let given point be A, B and C with positive vectors αˆi+βˆj+γˆk,βˆi+γˆj+αˆkandγˆi+αˆj+βˆk
As α,βandγ are distinct real numbers, therefore ABC form a triangle.
Clearly, AB=OB−OA=(βˆi+γˆj+αˆk)−(αˆi+βˆj+γˆk)
=(β−α)ˆi+(γ−β)ˆj+(α−γ)ˆk
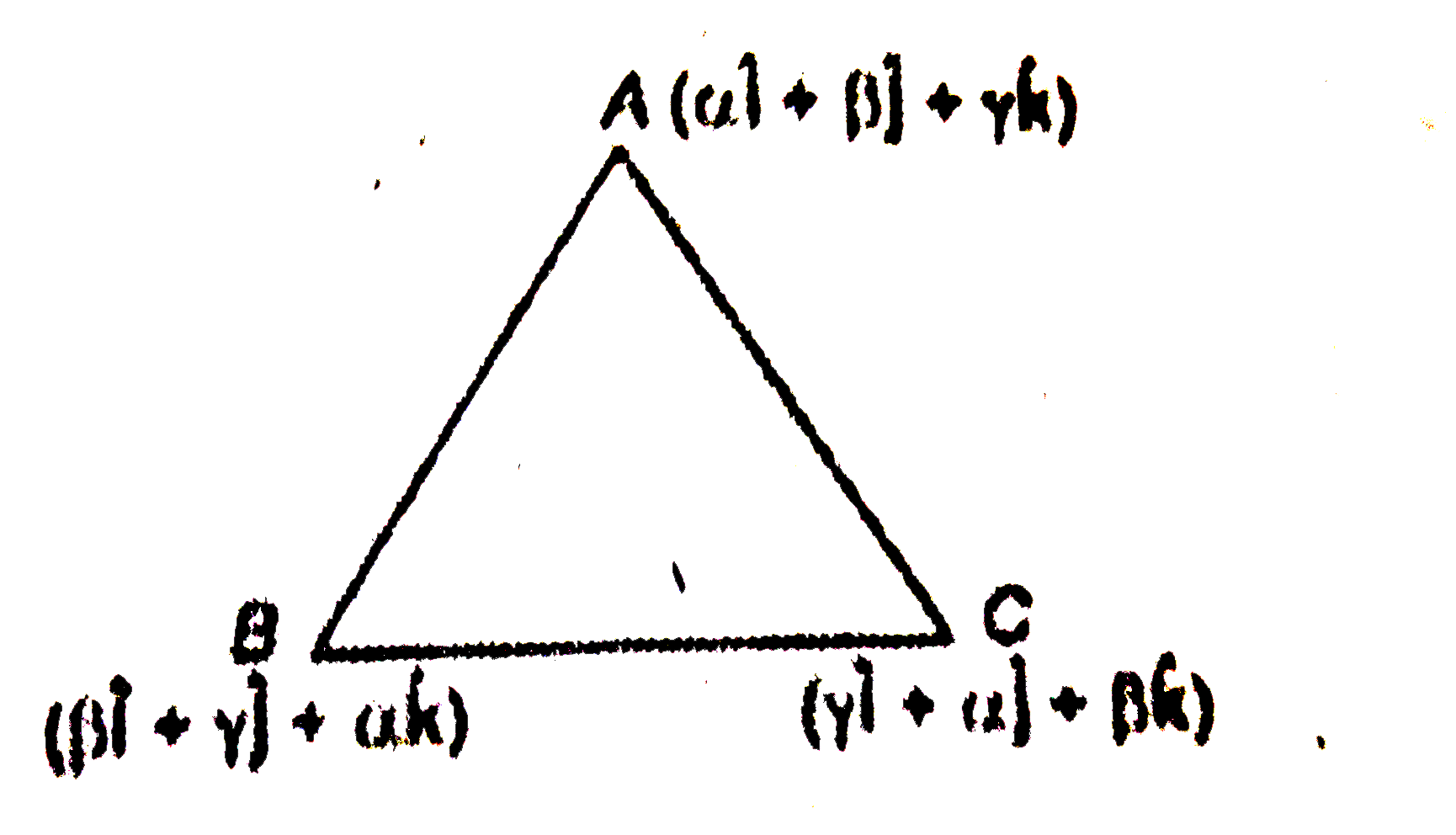
Now, |AB|=√(β−α)2+(γ−β)2+(α−γ)2
Similarly, BC=CA=√(β−α)2+(γ−β)2+(α−γ)2
∴ΔABC is an equilateral triangle.
Similar Questions
Let ˆα,ˆβ,ˆγbe three unit vectors such that ˆα×(ˆβ׈γ)=12(ˆβ+ˆγ) where ˆα×(ˆβ׈γ)=(ˆα.ˆγ)ˆβ−(ˆα.ˆβ)ˆγ. If ˆβ is not parallel to ˆγ, then the angle between ˆα and ˆβ is
View Solutionमाना →α=2ˆi+3ˆj−ˆk तथा →β=ˆi+ˆj है यदि →γ एक ईकाई सदिश है तो [→α×→β→β×→γ→γ×→α] का अधिकतम मान है
View SolutionLet ˆα,ˆβ,ˆγ be three unit vectors such that ˆα×(ˆβ׈γ)
=12(ˆβ+ˆγ) where ˆα×(ˆβ׈γ)=(ˆα.ˆγ)ˆβ−(ˆα.ˆβ)ˆγ. If ˆβ is not parallel to ˆγ, then the angle between ˆαandˆβ is
View SolutionLet a be a real number and →α=ˆi+2ˆj,→β=2ˆi+aˆj+10ˆk,→γ=12ˆi+20ˆj+aˆk be three vectors, then →α,→βand→γ are linearly independent for :
View SolutionLet α,β,γ are distinct real numbers. The points with position vectors αi+βj+γk, βi+γj+αk, γi+αj+βk
View SolutionConsider the vectors ˆi+cos(β−α)ˆj+cos(γ−α)ˆk,cos(α−β)ˆi+ˆj+cos(γ−β)ˆkandcos(α−γ)ˆi+cos(β−γ)ˆk+aˆkwhere α,β, and γ are different angles. If these vectors are coplanar, show that a is independent of α,β and γ
View SolutionLett α,βandγ be distinct real numbers. The points whose position vector's are αˆi+βˆj+γˆk;βˆi+γˆj+αˆkandγˆi+αˆj+βˆk
View SolutionConsider the vectors ˆi+cos(β−α)ˆj+cos(γ−α)ˆk,cos(α−β)ˆi+ˆj+cos(γ−β)ˆk and cos(α−γ)ˆi+cos(β−γ)ˆj+aˆkwhere α,β, and γ are different angles. If these vectors are coplanar, show that a is independent of α,β and γ
View Solution
