If →a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5,|→c|=7, then angle between →a and →b is Solution in Gujrati
A
π2
B
π3
C
π4
D
π6
Video Solution
Text Solution
The correct Answer is:B
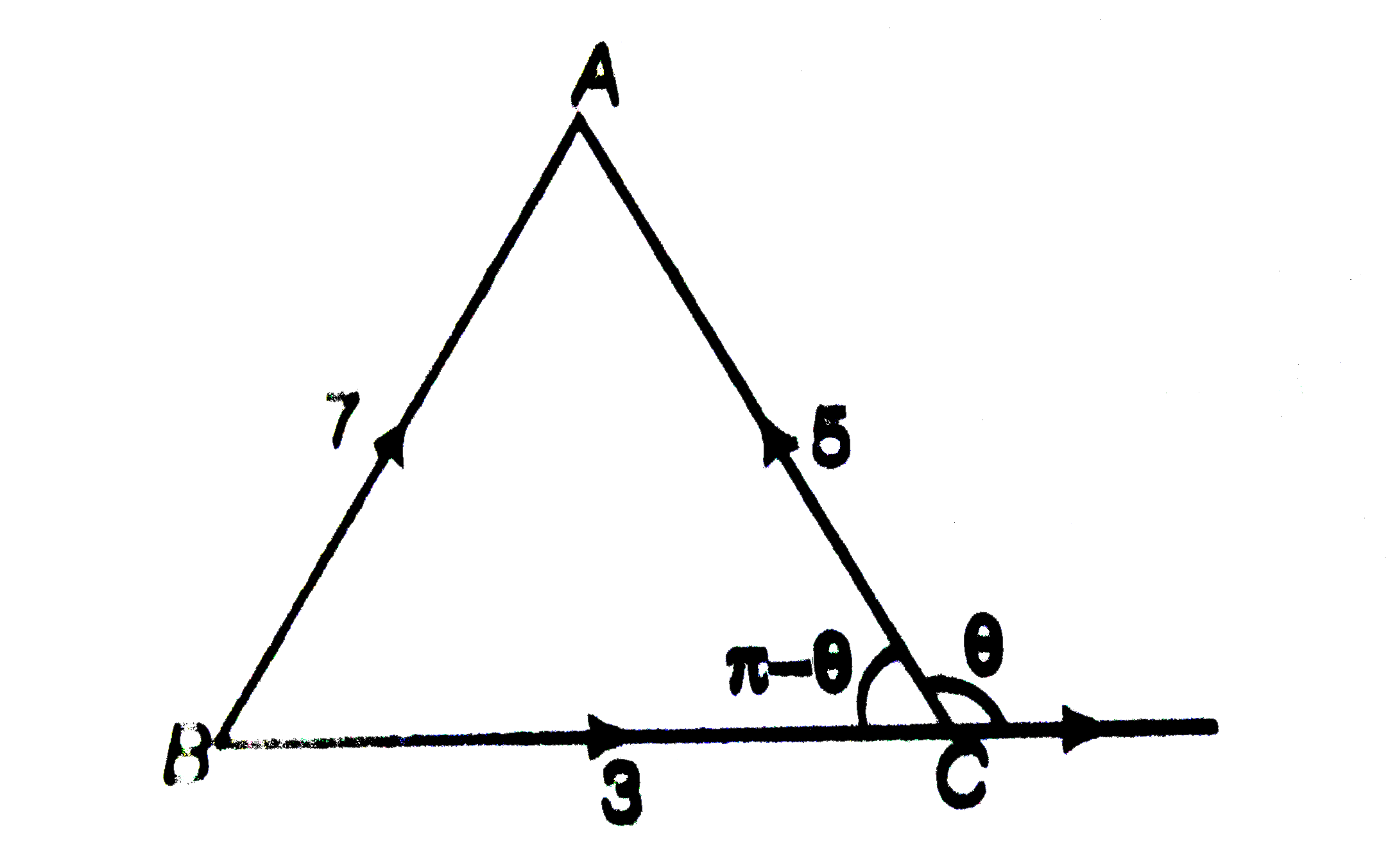
Let θ be the angle between a and b. then, ∠C=π−θ.
∴cos(π−θ)=32+52−722(3)(5)
∴−cosθ=−12
∴θ=60∘=π3
|
Similar Questions
→a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5,|→c|=9,find the angle between →a and →c.
View SolutionIf three unit vectors →a,→band→c satisfy→a+→b+→c=→0. Then find the angle between →aand→b.
View SolutionIf →a+→b+→c = →0,|→a| = 3 , ∣∣→b∣∣ = 5 and |→c| = 7, find the angle between →a and →b.
View SolutionVectors veca,vecb, vecc are such that veca + vecb + vecc = 0 and |veca| = 3, |vecb| = 5 and |vecc]= 7 . Find the angle between veca and vecb .
View SolutionIf →a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5and|→c|=7 , then the angle between →aand→b is
View Solution→a+→b+→c=→0,|→a|=3,∣∣→b∣∣=5,|→c|=9,find the angle between →a and →c.
View Solutionveca+vecb+vecc=vec0, |veca|=3, |vecb|=5,|vecc|=9 ,find the angle between veca and vecc .
View SolutionIf →a+→b+→c=→0 and |→a|=3,∣∣→b∣∣=5, and |→c|=7, find the angle between →a and →b.
View Solution
