Question

If $D,EandF$
are three points on the sides $BC,CAandAB,$
respectively, of a triangle $ABC$
such that AD,BE and CF are concurrent, then show that $\frac{BD}{CD},\frac{CE}{AE},\frac{AF}{BF}=-1$

Explanation

Here, D, E and F be the points on the sides BC,CA and AB respectively of `DeltaABC`. Such that points D,E and F are collinear, be shawn as the adjoining figuece.
Let B as the origin, BA=a and BC=c
The, BF=ka and BD=lc

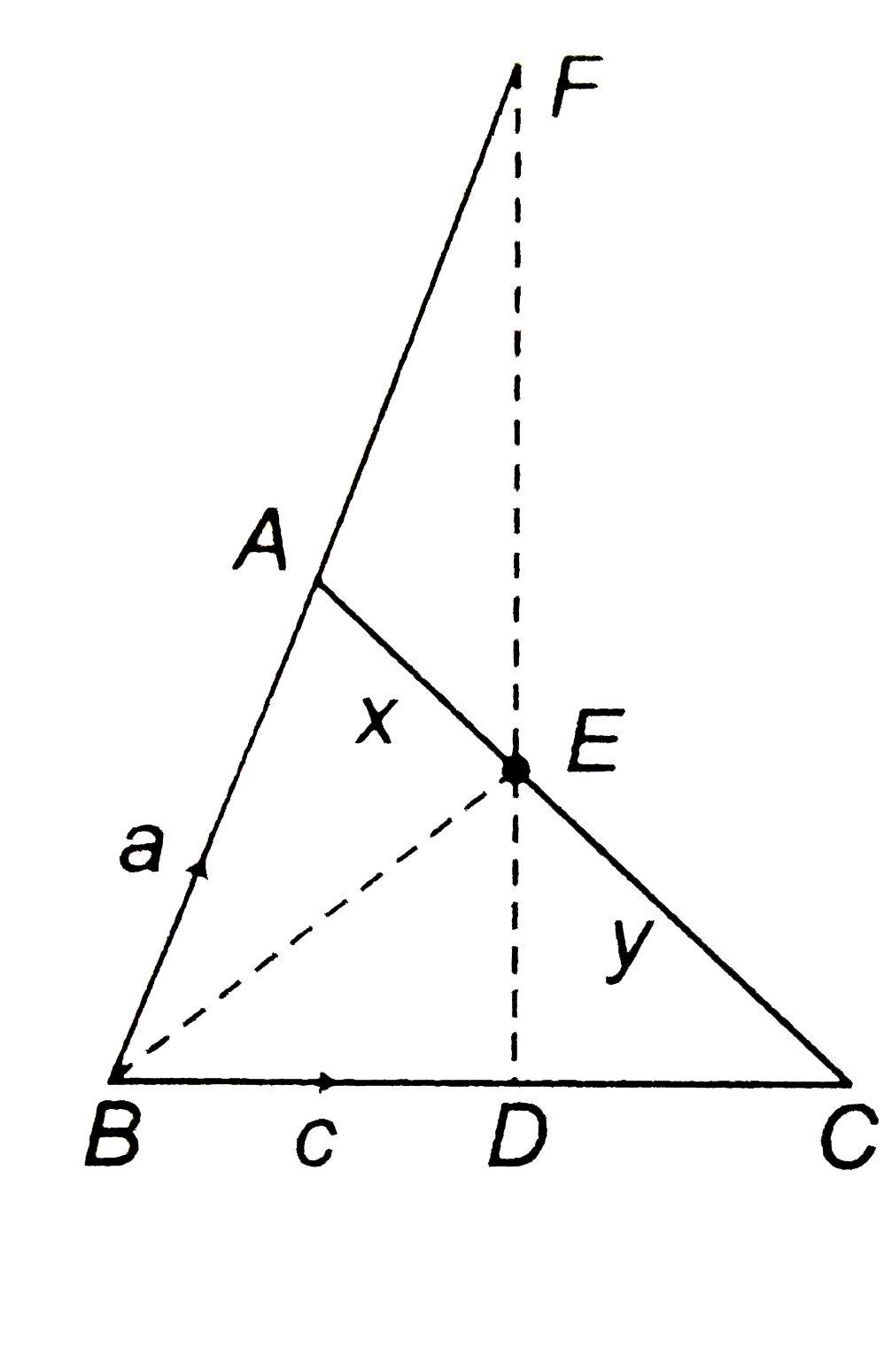
where, k and l are scalars.
`therefore(BD)/(BC)=l and (BF)/(BA)=k`
`impliesBC:BD=1:l`
`implies(BC)/(BD)-1=(1)/(l)-1implies(DC)/(BD)=(1-l)/(l)`
`implies(BD)/(DC)=(l)/(1-l) and (BA)/(BF)=(1)/(k)`
`implies1-(BA)/(BF)=1-(1)/(k)implies (AF)/(BF)=(k-1)/(k)`
Now, let E divide the line AC in the ratio of x:y
so, that `BE=(xc+ya)/(x+y)=(x*(BD)/(l)+y*(BF)/(k))/(x+y)`
`implies BE-(x)/(l(x+y))BD-(y)/(k(x+y))BF=0`
Since, D,E and F are collinear.
Sum of coefficient must be zero.
hence, `1-(x)/(l(x+y))-(y)/(k(x+y))=0`
`implies(x+y)-(x)/(l)-(y)/(k)=0impliex+y=(x)/(l)+(y)/(k)`
`implies x(1-(1)/(l))=y((1)/(k)-1)impliesx((l-1)/(l))=y((1-k)/(k))`
`implies (l)/(l-1)*(y)/(x)*(k-1)/(k)=1`
`implies(BD)/(DC)*(CE)/(AE)*(AF)/(BF)=1` [using Eqs. (i), (ii) and (iii)].