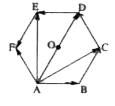
Consider the regular hexagon ABCDEF with centre at O (origin).
Five forces AB,AC,AD,AE,AF act at the vertex A of a regular hexagon ABCDEF. Then, their resultant isSolution in Gujrati
3AO
2AO
4AO
6AO
The correct Answer is:D
Consider the regular hexagon ABCDEF with centre at O (origin).

AD+EB+FC=2AO+2OB+2OC
=2(AO+OB)+2OC
=2AB+2AB [∵OC=AB]
=4AB
R=AB+AC+AD+AE+AF
=ED+AC+AD+AE+CD [∵AB=EDandAF=CD]
=(AC+CD)+(AE+ED)+AD
=AD+AD+AD=3AD=6AO
Similar Questions
If ABCDEF is a regular hexagon with centre O , then P.T ¯¯¯¯¯¯AB+¯¯¯¯¯¯AC+¯¯¯¯¯¯AD+¯¯¯¯¯¯AE+¯¯¯¯¯¯AF=3¯¯¯¯¯¯AD=6¯¯¯¯¯¯AO
View SolutionABCDEF is a regular hexagon with point O as centre. The value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF is:
View SolutionABCDEF is a regular hexagon with point O as centre. Find the value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF
View SolutionABCDEF is a regular hexagon with point O as centre. Find the value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF

View SolutionABCDEF is a regular hexagon with point O as centre. Find the value of −−→AB+−−→AC+−−→AD+−−→AE+−−→AF

View SolutionABCDEF is a regular hexagone. AB+AC+AD+AE+AF=λAD then λ = ………….
View SolutionABCDEF is a regular hexagon with point O as centre. Find the value of vec(AB)+vec(AC)+vec(AD)+vec(AE)+vec(AF) .
View SolutionIn a regular hexagon ABCDEF, prove that −−→AB+−−→AC+−−→AD+−−→AE+−−→AF=3−−→AD
View Solution
