If in a triangle PQR;sinP,sinQ,sinR are in A.P; thenSolution in Gujrati
the altitudes are in AP
the altitudes are in HP
the medians are in GP
the medians are in AP
The correct Answer is:B
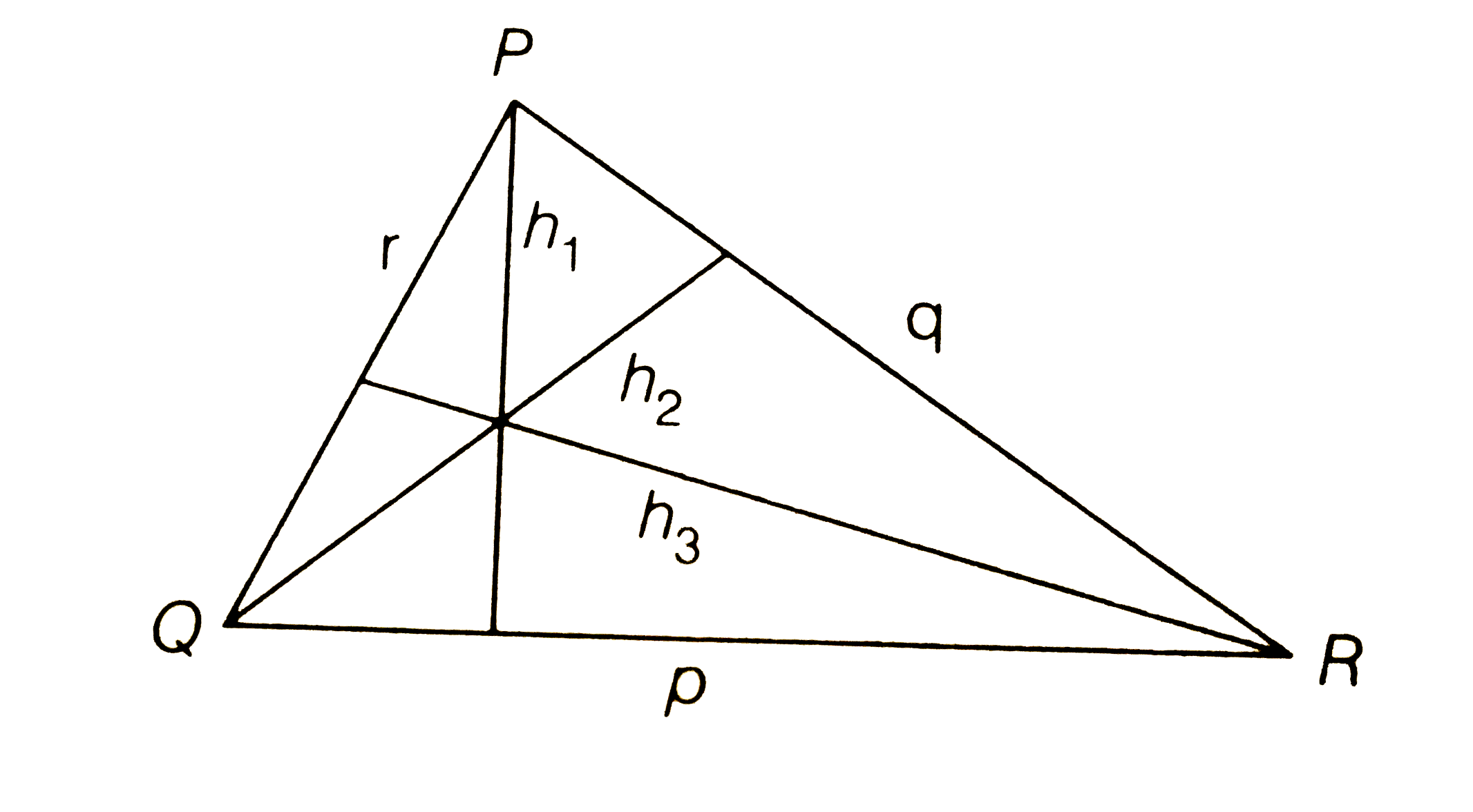
Let triangle be the area of ΔPQR.
∴Δ=12×p×h1 [h1,h2,h3 are altitudes ]
⇒h1=2Δp ….(i)
Similarly, h2=2Δq ….(ii)
and h3=2Δr ....(iii)
According to the question, sinP, sinQ, sin R are in AP.
Then, kp,kq,kr, are in AP [ by sine rule ]
⇒p,q,r are in AP.
⇒2Δh1,2Δh2,2Δh3 are in AP. [ by Eqs. (i),(ii) and (iii) ]
⇒1h1,1h2,1h3 are un AP.
⇒h1,h2,h3 are in HP.
⇒ Altitudes are in HP.
 .
.
Similar Questions
The triangle PQR of which the angles P,Q,R satisfy cos P =sinQ2sinR is :
View SolutionLet PQR be a triangle of area Δ with a=2,b=7/2, and c=5/2, where a, b and c are the lengths of the sides of the triangle opposite to the angles at P, Q and R, respectively. Then 2sinP−sin2P2sinP+sin2P equals
View SolutionIf Delta PQR If sin P sin Q sin R is in parallel range
View SolutionIn a ΔPQR , if 3 sin P+4 cos Q=6 and 4 sin Q+3 cos P=1 , then the angle R is equal to
View SolutionLet p,q,r be the sides opposite to the angles P,Q, R respectively in a triangle PQR if r2sinPsinQ=pq, then the triangle is
View SolutionLet PQR be a triangle of area Δ with a=2,b=7/2, and c=5/2, where a, b, and c are the lengths of the sides of the triangle opposite to the angles at P, Q, and R, respectively. Then 2sinP−sin2P2sinP+sin2P equals
View SolutionIf in a triangle PQR;sinP,sinQ,sinR are in A.P; then (A)the altitudes are in AP (B)the altitudes are in HP (C)the altitudes are in GP (D)the medians are in AP
View SolutionIf a ΔPQR if3sinP+4cosQ=6and4sinQ+3cosP=1, then∠R is equal to
View Solution
