Statement -1 (Assertion) and Statement - 2 (Reason)
Each of these examples also has four alternative choices,
ONLY ONE of which is the correct answer. You have to
select the correct choice as given below
Statement-1 If A and B are two matrices such
that AB = B, BA = A, then A2+B2=A+B.
Statement-2 A and B are idempotent matrices, then
A2=A,B2=B.Solution in Gujrati
Statement - 1 is true, Statement - 2 is true , Statement - 2
is correct explanaction for Statement -2
Statement -1 is true, Statement - 2 is true, Statement - 2
is not a correct explanation for Statement-2
Statement-1 is true, Statement-2 is false
Statement-1 is false, Statement-2 is ttrue
The correct Answer is:B
∵AB=B
⇒B(AB)=B⋅B
⇒(BA)B=B2 [ "by associative law"]
⇒AB=b2[∵BA=A]
⇒B=B2[∵AB=B]
and Ba = A
⇒A(BA)=A⋅A
⇒(AB)A+A2 [by associative law]
⇒BA=A2 [∵AB=B]
⇒A=A2[∵BA=A]
Hence, ∴A2+B2=A+B
Here, both statments are true and Statement - 2 is not a
correct explanation for Statement-1.
Similar Questions
Statement-1 (Assertion and Statement- 2 (Reason)
Each of these questions also has four alternative
choices, only one of which is the correct answer. You
have to select the correct choice as given below.
Statement-1 if A and B are two square matrices of order
n×n which satisfy AB=AandBA=B, then
(A+B)7=26(A+B)
Statement- 2 A and B are unit matrices.
View SolutionStatement-1 (Assertion and Statement- 2 (Reason)
Each of these questions also has four alternative
choices, only one of which is the correct answer. You
have to select the correct choice as given below.
Statement- 1 If A, B, C are matrices such that
|A3×3|=3,|B3×3|=−1and|C2×2|=2,|2ABC|=−12.
Statement - 2 For matrices A, B, C of the same order
|ABC|=|A||B||C|.
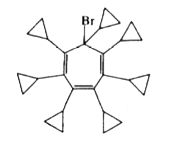
View SolutionIn the given compound, will Br ionize in the form of (a) Br^(-) or (b) Br^(+) .
View SolutionIn the given compound, will Br ionize in the form of (a) Br− or (b) Br+.
View SolutionStatement-1 (Assertion) and Statement- 2 (Reason)
Each of these questions also has four alternative
choices, only one of which is the correct answer. You
have to select the correct choice as given below.
Statement-1 if A and B are two square matrices of order
n×n which satisfy AB=AandBA=B, then
(A+B)7=26(A+B)
Statement- 2 A and B are unit matrices.
View SolutionStatement-1 (Assertion and Statement- 2 (Reason)
Each of these questions also has four alternative
choices, only one of which is the correct answer. You
have to select the correct choice as given below.
Statement- 1 If A, B, C are matrices such that
|A3×3|=3,|B3×3|=−1and|C2×2|=2,|2ABC|=−12.
Statement - 2 For matrices A, B, C of the same order
|ABC|=|A||B||C|.
View SolutionStatement-1 (Assertion and Statement- 2 (Reason)
Each of these questions also has four alternative
choices, only one of which is the correct answer. You
have to select the correct choice as given below.
Statement-1 if A and B are two square matrices of order
n×n which satisfy AB=AandBA=B, then
(A+B)7=26(A+B)
Statement- 2 A and B are unit matrices.
View SolutionStatement-1 (Assertion and Statement- 2 (Reason)
Each of these questions also has four alternative choices, only one of which is the correct answer. You have to select the correct choice as given below.
Statement-1 For a singular matrix A,ifAB=AC⇒B=C
Statement-2 If |A|=0, thhenA−1 does not exist.
a. Statement- is true, Statement -2 is true, Statement-2
is a correct explanation for Statement-1
b. Statement-1 is true, Statement-2 is true, Sttatement - 2
is not a correct explanation for Stamtement-1
c. Statement 1 is true, Statement - 2 is false
d. Statement-1 is false, Statement-2 is true
View Solution
