Statement-1 : The superposition of the waves y1=Asin(kx−ωt) and y2=3Asin(kx+ωt) is a pure standing wave plus a travelling wave moving in the negative direction along X-axis
Statement-2 : The resultant of y1 & y2 is y=y1+y2=2Asinkxcosωt+2Asin(kx+ωt).Solution in Gujrati
Statement-1 is true, Statement-2 is true , Statement-2 is correct explanation for Statement-7
Statement-1 is true,Statement-2 is true , Statement-2 is NOT a correct explanation for Statement-7
Statement-1 is true, Statement-2 is false
Statement-1 is false, Statement-2 is true
The correct Answer is:A
Step by step video & image solution for Statement-1 : The superposition of the waves y_(1) = A sin(kx - omega t) and y_(2) = 3A sin (kx + omega t) is a pure standing wave plus a travelling wave moving in the negative direction along X-axis Statement-2 : The resultant of y_(1) & y_(2) is y=y_(1) + y_(2) = 2A sin kx cos omega t + 2A sin (kx + omega t). by Physics experts to help you in doubts & scoring excellent marks in Class 11 exams.
Updated on:21/07/2023Topper's Solved these Questions
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[A]
29 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-04)[B]
13 Videos
- WAVES AND OSCILLATIONSBOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-02)
19 Videos
- SEMICONDUCTORSBOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)
50 Videos
Similar Questions
A stone dropped from the top of a tower of height 300 m high splashes into the water of a pond near the base of the tower. When is the splash heard at the top givne that the speed of sound in air is 340ms−1?(g=9.8ms−2)
View SolutionA source of sound is moving along a circular orbit of radius 3meter with an angular velocity of 10rad/s. A sound detector located far away from the source is executing linear simple harmonic motion along the line BD with an amplitude BC=CD=6meters. The frequency of oscillation of the detector is 5π per second. The source is at the point A when the detector is at the point B. If the source emits a continuous sound wave of frequency 340Hz, Find the maximum and the minimum frequencies recorded by the detector.
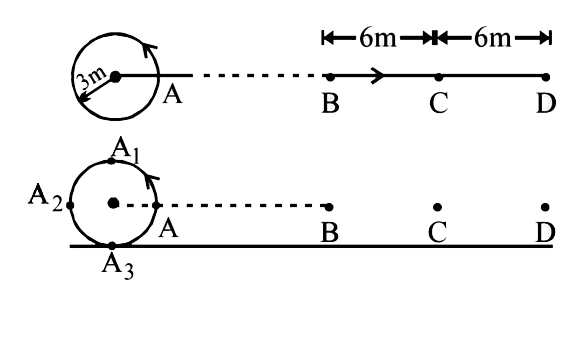
View SolutionA sound wave of frequency f travels horizontally to the right. It is reflected from a large vertical plane surface moving to left with a speed v. The speed of sound in medium is C
View SolutionAt absolute zero temperature Si acts as ……..
View SolutionLet the two waves y_(1) = A sin ( kx - omega t) and y_(2) = A sin ( kx + omega t) from a standing wave on a string . Now if an additional phase difference of phi is created between two waves , then
View SolutionTwo wave are represented by equation y_(1) = a sin omega t and y_(2) = a cos omega t the first wave :-
View SolutionTwo waves are given byy1=asin(ωt−kx) and y2=acos(ωt−kx). The phase difference between the two waves is
View SolutionWave equations of two particles are given by y_(1)=a sin (omega t -kx), y_(2)=a sin (kx + omega t) , then
View SolutionEquation of motion in the same direction are given by ltbygt y1=2asin(ωt−kx)andy2=2asin(ωt−kx−θ)
The amplitude of the medium particle will be
View SolutionEquation y=y_(0) sin (Kx+omega t) represents a wave :-
View SolutionThree waves y_(1), y_(2) ,y_(3) are given by y_(1)= A sin (Kx- omegat), y_(2) A= sin (Kx+ omega t) and y_(3) = A sin (Ky- omega t) . Which one of the following represents wave ?
View Solutiony_(1) = 4 sin (omega t + kx), y_(2) =-4 cos(omega t + kx) , the phase difference is
View SolutionTwo waves are represented by
y1=a1cos(ωt−kx) and
y2=a2sin(ωt−kx+π/3)
Then the phase difference between them is-
View SolutionTwo harmonic travelling waves are described by the equations y_(1)=a sin(kx-omega t) and y_(2)=a sin(-kx+omega t+phi) . The amplitude of the superimposed wave is
View Solutiony1=asin(ωt−kx) तथा y2=acos(ωt−kx) दो तरंगें दी गई हैं दोनों तरंगों के बीच कलान्तर है
View Solutionदो तरंगों के समीकरण है
y1=asin(ωt−kx) तथा y2=acos(ωt–kx)
दो तरंगों के बीच कलांतर है
View Solution
