For pure ''Ge'' semiconductor quantity of ''e'' and hole is 1019e/m3 if we doped donor impurity in it with density 1023e/m3 then quantity of hole (e/m3) in semiconductor is :-Solution in Gujrati
1015
1019
1023
1027
The correct Answer is:A
nh=n2ine=(1019)21023=1015
Topper's Solved these Questions
- BOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-2)49videos
SEMICONDUCTORS
- BOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-3)27videos
SEMICONDUCTORS
- BOOK - ALLEN CHAPTER - SEMICONDUCTORSEXERCISE - Part-3(Exercise-4)50videos
SEMICONDUCTORS
- BOOK - ALLEN CHAPTER - PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT EXERCISE - EXERCISE-IV7videos
PHYSICAL WORLD, UNITS AND DIMENSIONS & ERRORS IN MEASUREMENT
- BOOK - ALLEN CHAPTER - WAVES AND OSCILLATIONSEXERCISE - Part-1(Exercise-05)[B]42videos
WAVES AND OSCILLATIONS
Similar Questions
Find VAB
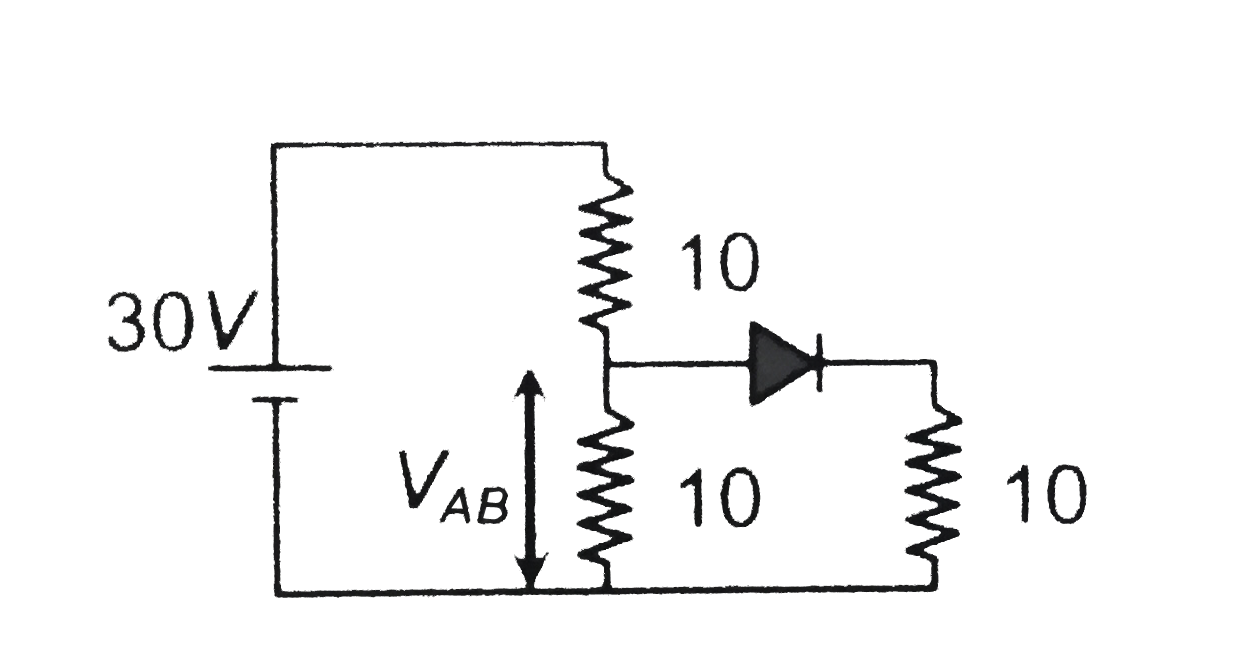 01:42View Solution
01:42View SolutionAssertion: Microwave communication is preferred to optical communication
Reason: Microwaves provide large number of channels and bandwidths as compared to optical signals.03:07View SolutionAt absolute zero temperature Si acts as ……..
02:50View SolutionAssertion : Gravitational forces do not depend on the medium between the masses.
Reason : Mediating particle responsible for gravitational force is graviton.02:31View SolutionA string of length 0.4m and mass 10−2kg is clamped at one end . The tension in the string is 1.6N. The identical wave pulses are generated at the free end after regular interval of time , Δt . The minimum value of Δt , so that a constructive interference takes place between successive pulses is
01:45View SolutionA pure semiconductor has equal electron and hole concentration of 10^(6)m^(-3) . Dopping by indium increases n_(h) to 4.5xx10^(22)m^(0k3) . What is n_(e) in the dopped semiconductor?
02:02View SolutionPure Si at 500K has equal number of electron (ne) and hole (nh) concentration of 1.5×1016m−3. Dopping by indium. Increases nh to 4.5×1022m−3. The doped semiconductor is of
01:33View SolutionA semiconductor has equal electron and hole concentration of 6xx 10^(4)m^(-3) . On doping with a certain impurity, electron concentration increases to 8 xx 10^(12)m^(-3) . Identify the type of semiconductor.
01:50View SolutionA semiconductor has equal electron and hole concertration 6xx10^(8) m^(-3) . On doping with a certain impurity electron concertration increase to 8xx10^(12) m^(-3) . Identify the type of semiconductor after doping.
02:26View SolutionThe number density of free electrons in the semiconductor is 1018m−3. It is doped with a pentavalent impurity atoms of number density 1024m−3, the number density of free electrons m−3 increases by a factor of
View SolutionA pure semiconductor has equal electron and hole concentration of 10^(16) m^(-3) . Doping by indium increases number of hole concentration n_(h) to 5 xx 10^(22) m^(-3) . Then, the value of number of electron concentration n_(e) in the doped semiconductor is
02:54View SolutionThe specimen of an intrinsic semiconductor contains 1.2xx10^15 holes/ m^3 . If it is doped by phosphorous atoms in a small proportion, then the number of holes/ m^3 in the doped semiconductor will
03:44View SolutionA semiconductor has equal electron and hole concentration of 2xx10^(8)m^(-3) . On doping with a certain impurity, the electron concentration increases to 4xx10^(10)m^(-3), then the new hole concentration of the semiconductor is
02:02View SolutionA semiconductor has equal electron and hole concentration of 2×108m−3. On doping with a certain impurity, the eletron concendration increases to 4×1010m−3, then the new hole concentration of the semiconductor is
03:00View SolutionIn an intrinsic semiconductor, the density of conduction electrons is 7.07×1015m−3 . When it is doped with indium, the density of holes becomes 5×1022m−3. Find the density of conduction electron is doped semiconductor
View SolutionThe number density of free electrons in the semiconductor is 10^(18) m^(-3) . It is doped with a pentavalent impurity atoms of number density 10^(24) m^(-3) . The number density of free electrons m^(-3) increases by a factor of
03:18View Solution

