A calorie is a unit of heat or energy and it equals about 4.2J,where1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals αkg, the unit of length equals is βm , the unit of time is γs. Show tthat a calorie has a magnitude 4.2α−1β−1γ2 in terms of the new units.Solution in Gujrati
4.18γ2αβ2
4.18αβ2γ2
4.18γ2α
4.18β2αγ2
The correct Answer is:A
I calorie =4.18J=4.18kg−m2/s2
=[4.18γ2αβ2](αkg)(βm)2(γs)2
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 3
92 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
The diagram shows the arrangement of three small uniformally charged spheres, A,B and C. The arrow indicate the direction of the electrostatic forces acting between the spheres (for example, the left arrow on sphere A indicates the electronstatic force on sphere A due to sphere B). At least two of the spheres are positively charged. Which sphere, if any, could be negatively charged?
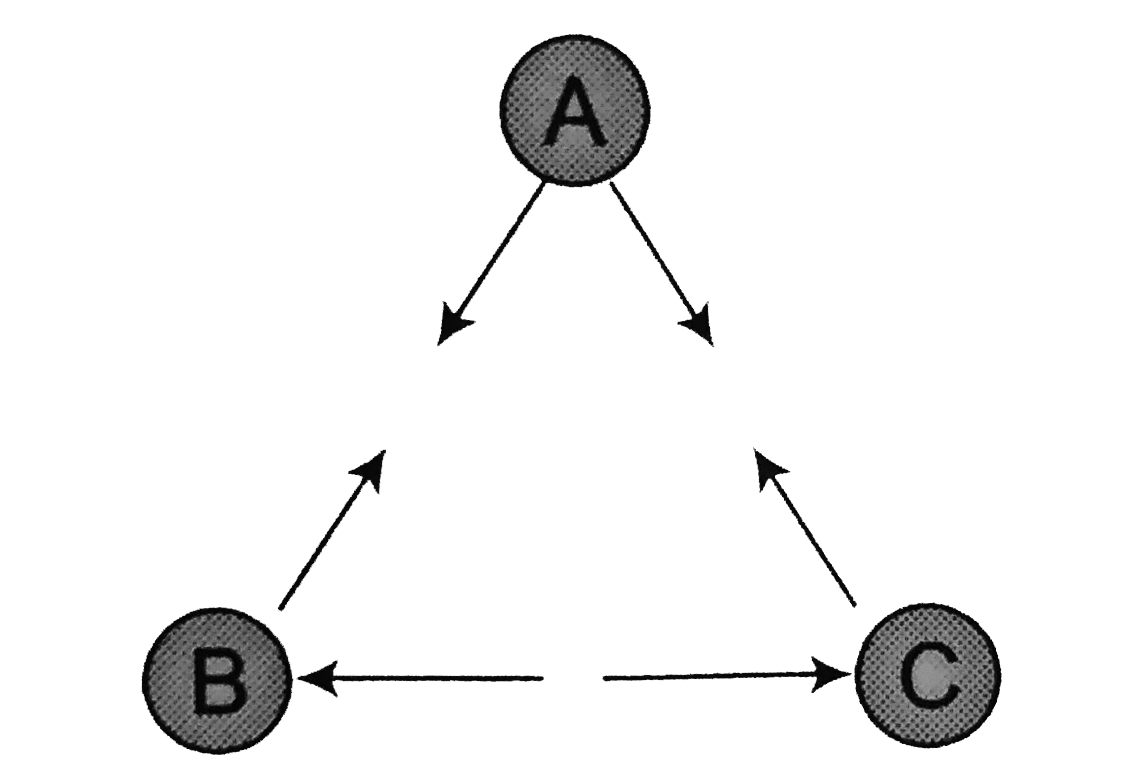
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View Solutionऊष्मा (परागमन में ऊर्जा) का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहाँ 1J=1kgm2s−2 | मान लीजिये कि हम मात्रकों की कोई ऐसी प्रणाली उपयोग करते हैं जिससे द्रव्यमान का मात्रक αkg के बराबर है, लंबाई का मात्रक के बराबर है, समय का मात्रक γs के बराबर है । यह प्रदर्शित कीजिये कि नए मात्रकों के पदों में कैलोरी का परिणाम 4.2α−1β−2γ2 है ।
View Solutionऊष्मा या ऊर्जा का मात्रक कैलोरी है और यह लगभग 4.2 J के बराबर है, जहाँ 1 J = 1 kg m2s−2 । मान लीजिए कि हम मात्रको कि कोई ऐसी प्रणाली उपयोग करते हैं जिससे द्रव्यमान का मात्रक α kg के बराबर है, लम्बाई का मात्रक βm के बराबर है, समय का मात्रक γ s के बराबर है । यह प्रदर्शित कीजिए कि न्य मात्रको के पदों में कैलोरी का परिमाण 4.2α−1β−2γ2 है ।
View SolutionIf mass is measured in unit of α kg, length in β m and time in γ s, then calorie would be
View SolutionA calorie is a unit of heat or energy and it equals about 4.2J,where1J=1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals αkg, the unit of length equals is βm , the unit of time is γs. Show tthat a calorie has a magnitude 4.2α−1β−1γ2 in terms of the new units.
View Solution1 calorie=4.2 J where IJ= 1 kg m^2s^-2 . Suppose we employ a system of units in which the unit of mass is alpha kg, the unit of length is beta m and the unit of time gamma s , show that a calorie has a magnitude 4.2alpha^-1beta^-2gamma^-2 in the new system.
View SolutionA calorie is a unit of heat or energy and it equals 4.2 J where 1J = 1 kg m^(2)s^(-2) . Suppose we employ a system of units in which unit of mass is alpha kg. unit of length is beta m, unit of time is gamma . What will be magnitude of calorie in terms of this new system?
View SolutionA calorie is a unit of heat (energy in transit) and it equals about 4.2 J where 1J= 1kgm2s−2. Suppose we employ a system of units in which the unit of mass equals α kg, the unit of length equals βm, the unit of time is γs. Show that a calorie has a magnitude 4.2α−1β−2γ2 in terms of the new units.
View SolutionIf the unit of mass is α kg, the unit of length is β metre and the unit of time is "γ' second, The magnitude of calorie in the new system is (1 Cal = 4.23)
View Solution1 calorie=4.2 J where IJ= 1 kg m2s−2. Suppose we employ a system of units in which the unit of mass is α kg, the unit of length is β m and the unit of time γs, show that a calorie has a magnitude 4.2α−1β−2γ−2 in the new system.
View SolutionIf the unit of mass is a kg, the unit of length is β metre and the unit of time is γ second, The magnitude of calorie in the new system is (1 Cal = 4.2 J)
View Solutionमात्रकों की एक नई प्रणाली का प्रस्ताव किया गया है जिसके द्रव्यमान का मात्रक αkg, लंबाई का मात्रक βm तथा समय का मात्रक γs है। इस नई प्रणाली में 5 J का माप क्या होगा ?
View Solutiona calorie is a unit of heat or energy and it equals about 4.2J, where 1J=1kgm^2s^(-2) . suppose we employ a system of units in which the unit of mass equals alpha kg, the unit of length equals beta meter, the unit of time is second. show that a calorie has a magnitude 4.2alpha^(-1)beta^(-2)gamma^2 in terms of new units.
View Solution
