A wide vessel with small hole in the bottom is filled with water and kerosence, Neglecting viscosity, the velocity of water flow v, if the thickness of water laer is H1 and that of kerosene layer is H2 is (density of water P1g/ and that of kerosene is P2g/.Solution in Gujrati
v=√2g(h1+h2)
v=√2g(h1p1+h2p2)
v=√2g[h1+h2(p2p2)+h2]
v=√2g[h1(p1p2)+h2]
The correct Answer is:C
Applying bernoulis theorem for point 1 and 2
p1gh1+p2gh2+12pv2+P0
=0+12p1v2+P0(v<<v2)
p1gh1+p2gh2=12p1v2
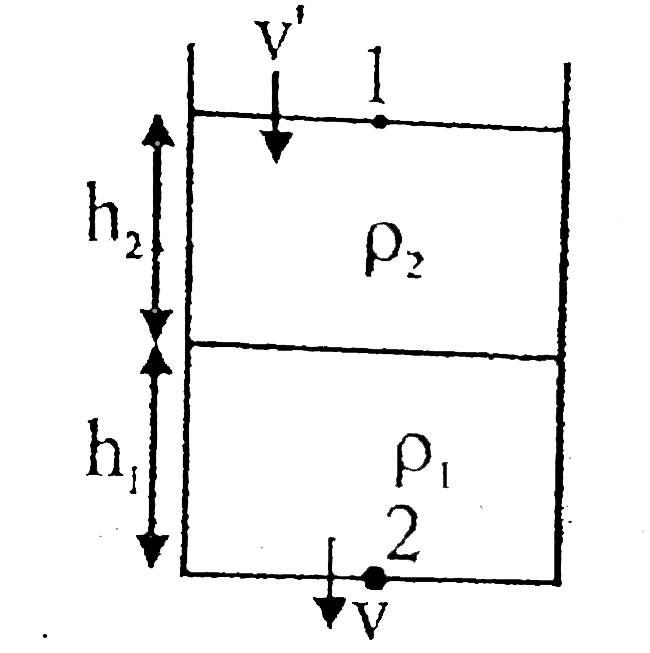
v=√2g[h1+h2(p2p1)]
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 3
92 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
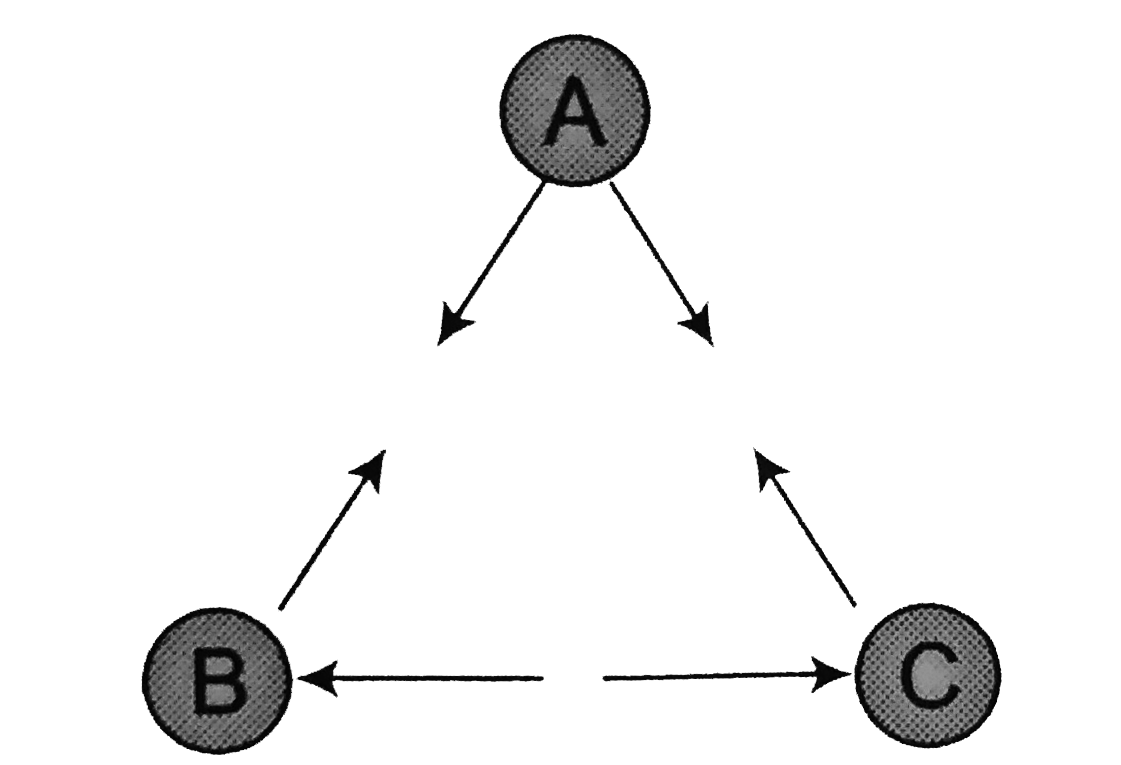
The diagram shows the arrangement of three small uniformally charged spheres, A,B and C. The arrow indicate the direction of the electrostatic forces acting between the spheres (for example, the left arrow on sphere A indicates the electronstatic force on sphere A due to sphere B). At least two of the spheres are positively charged. Which sphere, if any, could be negatively charged?
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA wide vessel with a small hole in the bottom is filled with water and kerosene. Find the velocity of water flow if the thickness of water layer is h1=30cm and that of kerosene is h2=20cm brgt

View SolutionA wide cylindrical tank with a small opening in the bottom has a water column of height h_(1) and above the water column, there is a layer of kerosene oil of thickness h_(2). The velocity of efflux through the opening is
View SolutionA wide vessel with a small hole in the bottom is filled with water and kerosene. Neglecting the viscosity, find the velocity of the water flow, if the thickness of the water layer is equal to h1=30cm and that of the keroscene layer to h2=20cm.
View SolutionA vessel is filled with water and kerosence oil. The vessel has a small hole in the bottom. Neglecting viscosity if the thickness of water layer is h1 and kerosens layer is h2 then the velocity v of flow of water will be (density of water is ρ1b g/c c and that of kerosense is ρ2 g/c c
View SolutionA beaker contains water up to a height h1 and kerosene of height h2 above water so that the total height of (water + kerosene) is (h1+h2) . Refractive index of water is μ1 and that of kerosene is μ2 . The apparent shift in the position of the bottom of the beaker when viewed from above is :-
View Solutionएक बीकर में जल ऊँचाई h1 तक और उसके ऊपर मिट्टी का तेल ऊँचाई h2 तक इस प्रकार भरा है कि जल व मिट्टी के तेल कि कुल ऊँचाई h1+h2 है | पानी का अपवर्तनांक μ1 व मिट्टी के तेल का अपवर्तनांक μ2 है | ऊपर से देखे जाने पर बीकर की तली की स्थिति में आभासी उठाव होगा :
View SolutionA wide vessel of uniform cross- section with a small hole in the bottom is filled with 40cm thick layer of water and 30cm thick layer of kerosene.The relative density of kerosene is 0.8 .The initial velocity of flow of water streaming out of the hole is (take g=10ms^(-2) )
View SolutionA wide vessel of uniform cross-section with a small hole in the bottom is filled with "40cm thick layer of water and "30cm" thick layer of kerosene.The relative density of kerosene is "],[0.8" .The initial velocity of flow of water streaming out of the hole is (take g=10ms−2
View SolutionA tank with a small hole at the bottom has been filled with water and kerosene (specific gravity 0.8). The height of water is 3 m and that of kerosene 2 m. When the hole is opened the velocity of fluid coming out from it is nearly: ("take g = 10 ms"^(-2)" and density of water "=10^(3)" kg m"^(-3))
View SolutionA breaker contains water up to a height h_(1) and kerosene of height h_(2) above water so that the total height of (water + kerosene) is (h_(1) + h _(2)) . Refractive index of water is mu_(1) and that of kerosene is mu_(2) . The apparent shift in the position of the bottom of the beaker when viewed from above is :
View SolutionThe density of water is 1 g/cc. This is strictly valid at
View SolutionA large vessel with a small hole at the bottom is filled with water and kerosene. The height of he water column is 20 cm and that of the kerosene is 25 cm. The velocity with which water flows out of the hole is (density of kerosene = 0.8 gm/cc) (Neglect viscous forced)
View Solution
