Assertion:- A particle is moving in a circle with constant tangential acceleration such that its speed v is increasing. Angle made by resultant acceleration of the particle with tangential acceleration increases with time.
Reason:- Tangential acceleration =∣∣∣d→vdt∣∣∣ and centripetal acceleration =v2RSolution in Gujrati
If both Assertion & Reason are True & the Reason is a correct explanation of the Assertion.
If both Assertion & Reason are True but Reason is not a correct explanation of the Assertion.
If Assertion is True but the Reason is False.
If both Assertion & Reason are False.
The correct Answer is:C
Step by step video & image solution for Assertion:- A particle is moving in a circle with constant tangential acceleration such that its speed v is increasing. Angle made by resultant acceleration of the particle with tangential acceleration increases with time. Reason:- Tangential acceleration =|(dvecv)/(dt)| and centripetal acceleration =(v^(2))/(R) by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 3
92 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
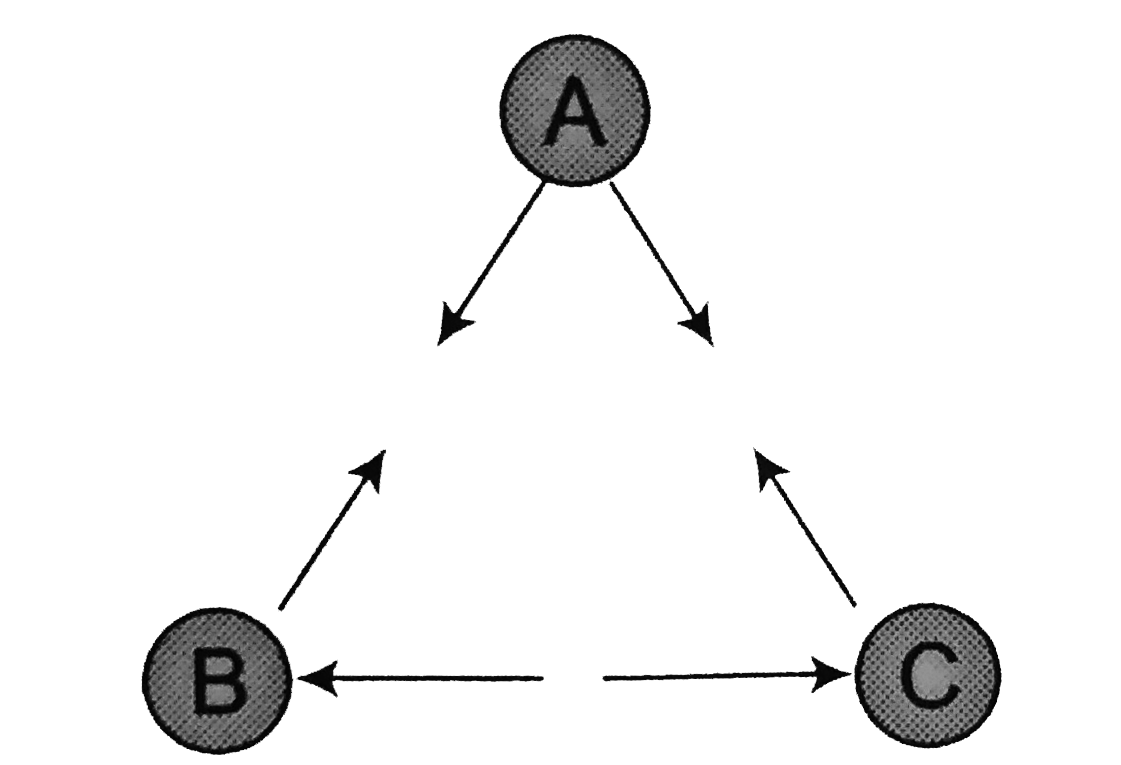
The diagram shows the arrangement of three small uniformally charged spheres, A,B and C. The arrow indicate the direction of the electrostatic forces acting between the spheres (for example, the left arrow on sphere A indicates the electronstatic force on sphere A due to sphere B). At least two of the spheres are positively charged. Which sphere, if any, could be negatively charged?
View SolutionA satellite S is moving in an elliptical orbit around the earth. The mass of the satellite is very small compared to the mass of the earth.
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionA particle moves on a circle of radius r with centripetal acceleration as function of time as ac=k2rt2, where k is a positive constant. Find the following quantities as function of time at an instant :
(a) The speed of the particle
(b) The tangential acceleration of the particle
( c) The resultant acceleration, and
(d) Angle made by the resultant with tangential direction.
View SolutionA particle is moving in a circle of radius R and its speed is given by v=lambdat^(2) , where lambda is a constant. Find (a) radial acceleration, (b) tangential acceleration, ( c) resultant acceleration and (d) angle between acceleration and velocity.
View SolutionA particle is moving with speed v=2t2 on the circumference of a circle of radius R. Match the quantities given in Table-1 with corresponding results in Table-2
Table-1Table-2(A)Magnitude to tangential acceleration of particle(P)decreases with time(B)Magnitude of centripetal acceleration of particle(Q)increases with time(C)Magnitude of angular speed of particle with respect to centre of circle(R)remains constant(D)Angle between the total acceleration and centripetal acceleration of partilce(S)depends upon the value of radius R
View SolutionA particle moves along a circle of radius r with constant tangential acceleration. If the velocity of the particle is v at the end of second revolution, after the revolution has started, then the tangential acceleration is
View SolutionIf the tangential acceleration of a particle around a circular path is 0.5ms−2 and radial acceleration is 0.65ms−2, then calculate the resultant acceleration of the particle.
View SolutionAssertion : For uniform circular motion it is necessary the speed of the particle is constant.
Reason : There is no tangential force or tangential acceleration acting on particle in uniform circular motion.
View SolutionA particle moves in a circle with constant tangential acceleration starting from rest. At t = 1/2 s radial acceleration has a value 25% of tangential acceleration. The value of tangential acceleration will be correctly represented by
View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
View SolutionA particle moves along a circle of radius'r' with constant tangential acceleration. If the velocity of the particle is 'v' at the end of second revolution , after the revolution has started then the tangential accleration is
View SolutionA particle is moving with speed v=2t2 on the circumference of a circle of radius R. Match the quantities given in Table-1 with corresponding results in Table-2
Table-1Table-2(A)Magnitude to tangential acceleration of particle(P)decreases with time(B)Magnitude of centripetal acceleration of particle(Q)increases with time(C)Magnitude of angular speed of particle with respect to centre of circle(R)remains constant(D)Angle between the total acceleration and centripetal acceleration of partilce(S)depends upon the value of radius R
View SolutionA particle moves on a circle of radius r with centripetal acceleration as function of time as a_c = k^2 r t^2 , where k is a positive constant. Find the following quantities as function of time at an instant : (a) The speed of the particle (b) The tangential acceleration of the particle ( c) The resultant acceleration, and (d) Angle made by the resultant acceleration with tangential acceleration direction.
View SolutionA particle is moving on a circle of radius A .At an instant its speed and tangential acceleration are B and C respectively.Total acceleration of the particle at that instant is
View Solution
