If uncertainty principle is applied to an object of mass 1 miligram, the product of uncertainly in velocity and position will be: Solution in Gujrati
The correct Answer is:C
Topper's Solved these Questions
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - Part-1 Physics
15 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - part-2 physics
73 Videos
- TEST PAPERSBOOK - ALLEN CHAPTER - TEST PAPERSEXERCISE - PAPER 2
60 Videos
- TEST PAPER 4BOOK - ALLEN CHAPTER - TEST PAPER 4EXERCISE - PHYSICS
45 Videos
- UNIT & DIMENSIONS, BASIC MATHS AND VECTOR BOOK - ALLEN CHAPTER - UNIT & DIMENSIONS, BASIC MATHS AND VECTOR EXERCISE - Exercise (J-A)
7 Videos
Similar Questions
A quantity of 2 mole of helium gas undergoes a thermodynamic process, in which molar specific heat capacity of the gas depends on absolute temperatureT , according to relation:
C=3RT4T0
where T0 is initial temperature of gas. It is observed that when temperature is increased. volume of gas first decrease then increase. The total work done on the gas until it reaches minimum volume is :-
View SolutionA bead is connected with a fixed disc of radius R by an inextensible massless string in a smooth horizontal plane. If the bead is pushed with a velocity v0 prependicular to the string, the bead moves in a curve and consequently collapses on the disc. Then

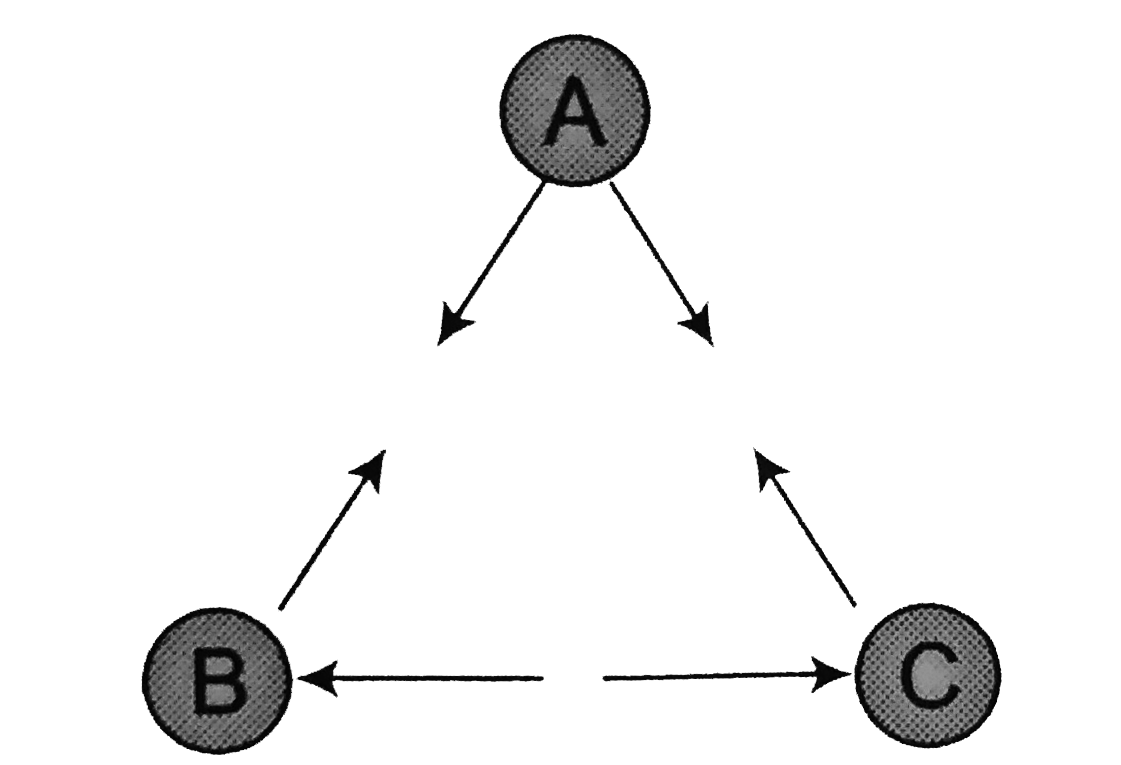
View SolutionThe diagram shows the arrangement of three small uniformally charged spheres, A,B and C. The arrow indicate the direction of the electrostatic forces acting between the spheres (for example, the left arrow on sphere A indicates the electronstatic force on sphere A due to sphere B). At least two of the spheres are positively charged. Which sphere, if any, could be negatively charged?
View SolutionTwo forces, each of magnitude F have a resultant of the same magnitude F. The angle between the two forces is
View SolutionMatch List I with List II and select the correct answer using the codes given below the lists :

View SolutionAccording to Heisenberg's uncertainly principle, the product of uncertainties in position and velocities for an electron of mass 9.1×10−31kg is.
View SolutionIf uncertainty principle is applied to an object of mass 1 miligram, the product of uncertainly in velocity and position will be:
View SolutionIf uncertainty principle is applied to an object of mass 1 miligram, the product of uncertainly in velocity and position will be:
View SolutionCalculate the product of uncertainty in position and velocity for an electron of mass 9.1 xx 10^(-31)kg according to Heisenberg uncertainty principle
View SolutionCalculate the product of uncertainties in the position and velocity of an electron of mass 9.1xx10^(-31)kg , according to Heisenberg's uncertainty principle.
View SolutionFor an electron whose positional uncertainly is 1.0xx10^(-10)m , the uncertainty in the component of the velocity in ms^(-1) will be
View SolutionWhen uncertainty in position and momentum are equal, then the uncertainly in velocity is
View SolutionUsing the uncertainty principle to determine the product of the uncertainty of the position and velocity of a moving electron.
View SolutionCalculate the product of uncertainity in position and velocity for an electron of mass 9.1×10−31 kg according to Heisenberg uncertainty principle.
View SolutionCalculate the product of uncertainity in position and velocity for an electron of mass 9.1×10−31 kg according to Heisenberg uncertainty principle.
View SolutionCalculate the product of uncertainity in position and velocity for an electron of mass 9.1×10−31 kg according to Heisenberg uncertainty principle.
View Solution
