Two particles of masses m1 and m2 in projectile motion have velocities →v1 and →v2 , respectively , at time t=0. They collide at time t0. Their velocities become →v'1 and →v'2 at time 2t0 while still moving in air. The value of ∣∣∣(m1→v'1+m2→v'2)−(m1→v1+m2→v2)∣∣∣Solution in Gujrati
The correct Answer is:C
By applying impulse-momentum theorem
=|(m1→v1+m2→v2)−(m1→v1+m2→v2)|
=|(m1+m2)→g(2L0)|−2(m1+m2)gt0
Topper's Solved these Questions
- CENTRE OF MASSBOOK - ALLEN CHAPTER - CENTRE OF MASSEXERCISE - EXERCISE-V A
20 Videos
- BASIC MATHEMATICS USED IN PHYSICS &VECTORS BOOK - ALLEN CHAPTER - BASIC MATHEMATICS USED IN PHYSICS &VECTORS EXERCISE - EXERCISE-IV ASSERTION & REASON
11 Videos
- ELASTICITY, SURFACE TENSION AND FLUID MECHANICSBOOK - ALLEN CHAPTER - ELASTICITY, SURFACE TENSION AND FLUID MECHANICSEXERCISE - Exercise 5 B (Integer Type Questions)
3 Videos
Similar Questions
Two identical particles move towards each other with velocity 2v and v respectively. The velocity of centre of mass is
View SolutionAssertion: If the initial and final positions coincide, the displacement is a null vector.
Reason: A physical quantity can not be called a vector, if its magnitude is zero.
View SolutionTwo soap bubbles A and B are kept in a closed chamber where the air is maintained at pressure 8N/m2.The radii of bubbles A and B are 2cm and 4cm, respectively. Surface tension of the soap-water used to make bubbles is 0.04N/m. Find tha ratio nB/nA, where nA and nB are the number of moles of air in bubbles A and B, respectively. [Neglect the effect of gravity.]
View Solution(1+|→u|2)(1+|→v|2)=(1−→u.→v)2+(→u+→v+(→u×→v)∣∣2
View SolutionIf →v1+→v2 is perpendicular to →v1−→v2, then
View SolutionFoe an arbitrary motion in sparce, which ot the following relations are true :
(a0 −−−−−−→avera≥=12[→v(t10+→v(t2)]
(b) →–––(avera≥)=[→r9t2)−→r(t−10]/(t2−t10
(c ) →v(t)=→v(0)+→at
(d) →r9t)=→r90)+→v(0)t+(1/2)→at2
(e) →aavera≥=[→v(t2)−→v(t−2)]/(t2−t1)1<br>Theavera≥standsforavera≥ofthewuantityoverthetime∫erval t_1andt2 ].
View SolutionTwo particles of masses m_(1) and m_(2) in projectile motion have velocities vec(v)_(1) and vec(v)_(2) , respectively , at time t = 0 . They collide at time t_(0) . Their velocities become vec(v')_(1) and vec(v')_(2) at time 2 t_(0) while still moving in air. The value of |(m_(1) vec(v')_(1) + m_(2) vec(v')_(2)) - (m_(1) vec(v)_(1) + m_(2) vec(v)_(2))|
View SolutionA moving particle of mass m collides elastically with a stationary particle of mass 2m. After collision the two particles move with velocity →v1 and →v2 respectively. Prove that →v2 is perpendicular to (2→v1+→v2)
View SolutionIn the Fig. shown pulley moves with acceleration →vP. Let acceleration of blocks m1 and m2 w.r.t. ground are →v1 and
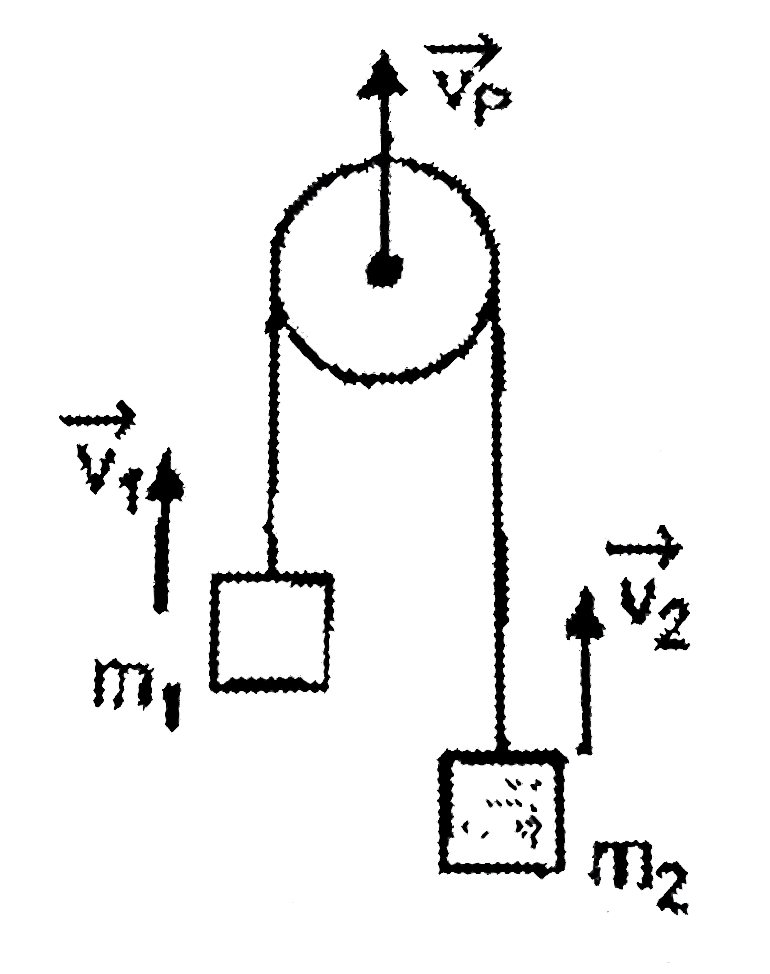
View SolutionIf two bodies are in motion with velocity →v1 and →v2:
View SolutionIf ∣∣→V1+→V2∣∣=∣∣→V1−→V2∣∣andV2 is finite, then
View Solutionप्रक्षेप्य गति में m1वm2 द्रव्यमानो के कणो के वेग समयt =0 पर क्रमशः →v1व →v2 है। ये समय t0पर टकराते है। उनके वेग समय 2t0 पर →v1 व→v2 हो जाते है जबकि अभी भी वे हवा में गतिमान है। तो
View SolutionA nucleus moving with a velocity vec(v) emits an alpha - particle. Let the velocities of the alpha - particle and the remaining nucleus be vec(v)_(1) and vec(v)_(2) and their masses be m_(1) and m_(2) .
View Solutionm1 व m2 द्रव्यमान के दो कण एक प्रक्षेप्य गति v1 में v2 वेग से गतिशील हैं। t=t0 समय पर टकराते हैं (प्रारम्भ से) तत्पश्चात् 2t0 समय पर उनकी वेग क्रमशः v'1 व v'2 पर हो जाते हैं, तब
[(m1v'1+m2v'2)−(m1v1−m2v2)]=?
View Solutionकिन्हीं दो सदिश →u तथा →v के लिए, निम्न सिद्ध कीजिए
(a) (→u.→v)2+|→u×→v|2=|→u|2|→v|2
(b)(1+|→u|2)(1+|→v|2)=(1−→u.→v)2+|→u+→v+(→u×→v)|2
View SolutionA nucleus moving with a velocity →v emits an α - particle. Let the velocities of the α - particle and the remaining nucleus be →v1 and →v2 and their masses be m1 and m2.
View Solution
