Rank in order, from largest to smallest, the sizes of the friction forces →fa to →fc in these 5 different situation. The box and the floor are made of the same materials in all situations.
(a) 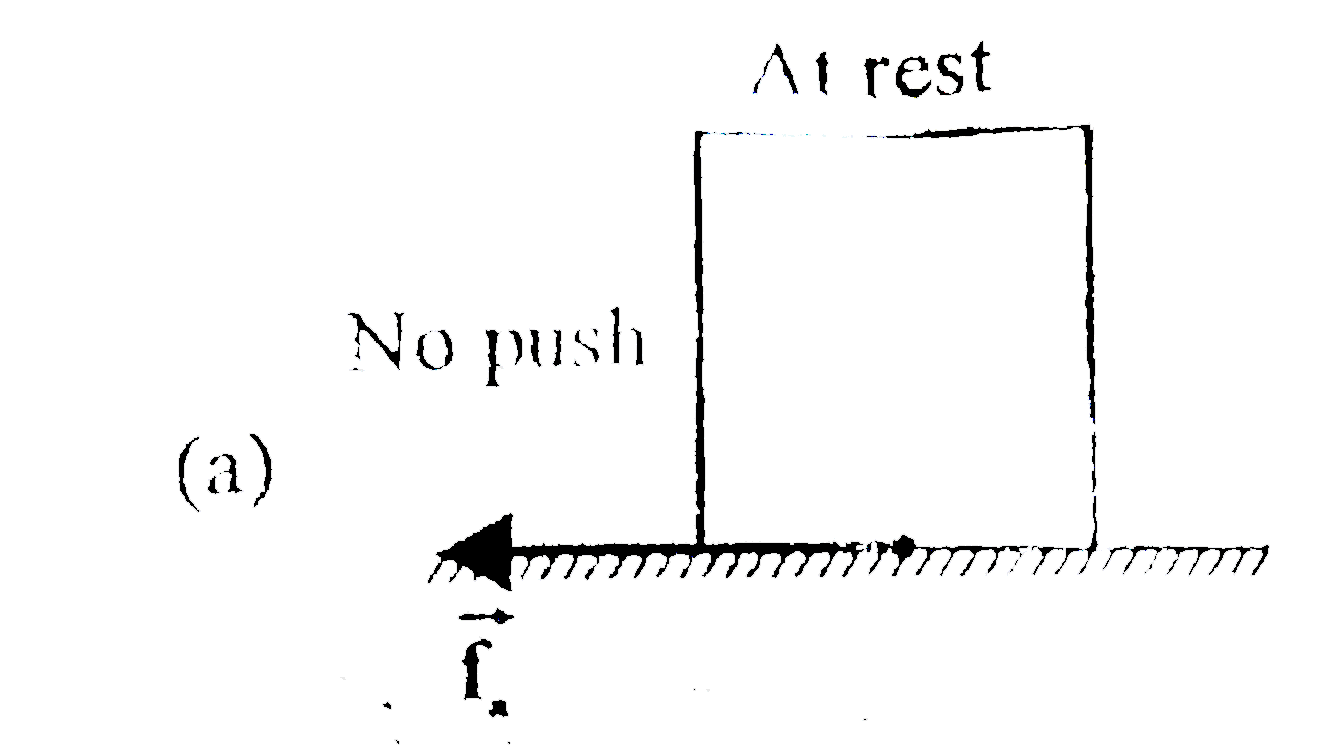
(b) 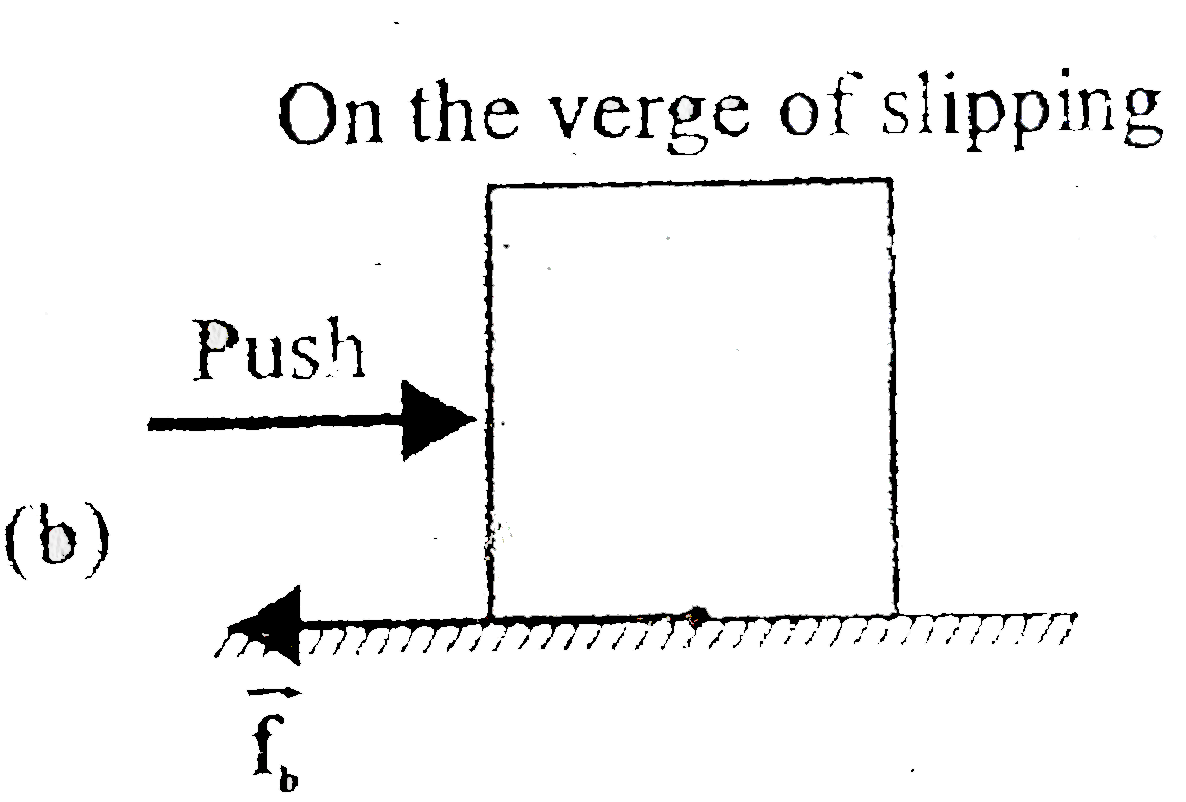
(c) 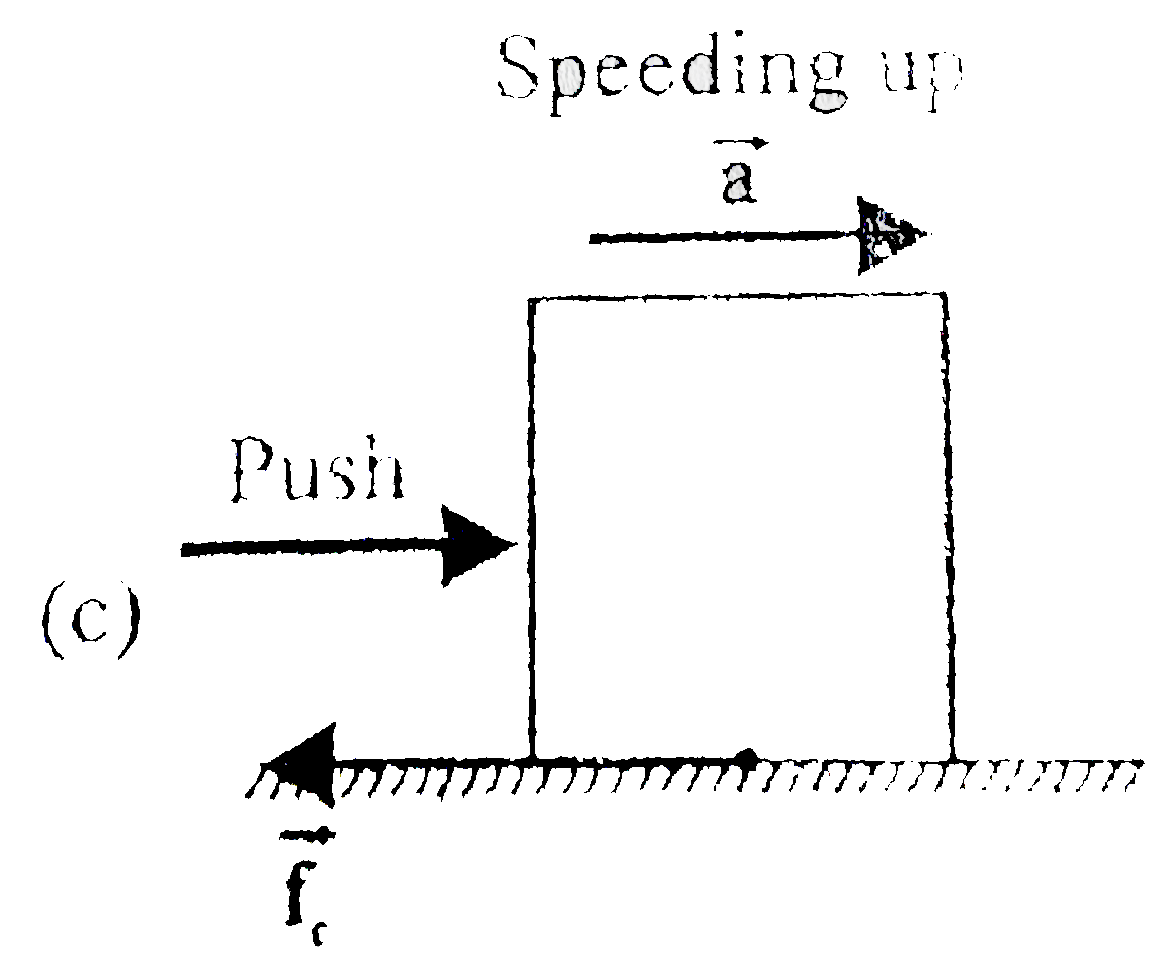
(d) 
(e)  Solution in Gujrati
Solution in Gujrati
fd<fb=fc=fc>fa
fc<fb=fd=fc>fa
fb=fc=fd=fc>fa
fb>fc=fd=fc>fa
The correct Answer is:D
fb>fc>fd>fe>fa Situations c ,d and e are all kinetic frIction, which does not depend on either velocity ot accerleration. Kinetic friction is smaller than the masimum static friction that is exerted in b, fa−0 because no friction is needed to keep the object at rest.
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionABCDE is pentagon, prove that →AB + →BC + →CD + →DE+→EA = →0 →AB+→AE+→BC+→DC+→ED+→AC=3→AC
View SolutionTwo forces →AB and →AD are acting at vertex A of a quadrilateral ABCD and two forces →CB and →CD at C prove that their resultant is given by 4→EF , where E and F are the midpoints of AC and BD, respectively.
View SolutionIn a regular hexagon ABCDEF, −−→AB=a, −−→BC=→b , −−→CD=c Then\ →AE=
View SolutionIf D, E, F are the midpoints of BC, CA, AB of Δ ABC, then →AD+→BE+→CF=
View SolutionTwo forces →AB and →AD are acting at vertex A of a quadrilateral ABCD and two forces →CB and →CD at C prove that their resultant is given by 4→EF , where E and F are the midpoints of AC and BD, respectively.
View SolutionABCDE is a pentagon. Prove that the resultant of force →AB, →AE ,→BC ,→DC ,→ED and →AC ,is 3→AC .
View SolutionABCDE is pentagon, prove that →AB + →BC + →CD + →DE+→EA = →0 →AB+→AE+→BC+→DC+→ED+→AC=3→AC
View SolutionTwo forces →AB and →AD are acting at vertex A of a quadrilateral ABCD and two forces →CB and →CD at C prove that their resultant is given by 4→EF , where E and F are the midpoints of AC and BD, respectively.
View SolutionABCDE is pentagon, prove that →AB + →BC + →CD + →DE+→EA = →0 →AB+→AE+→BC+→DC+→ED+→AC=3→AC
View SolutionIf ABCD is quadrilateral and EandF are the mid-points of ACandBD respectively, prove that →AB+→AD +→CB +→CD =4 →EF.
View SolutionIn a regular hexagon ABCDEF, A→B=a, B→C=→b and →CD=c Then\ →AE=
a.→a+→b+→c b. 2→a+→b+→c c. →b+→c d. →a+2→b+2→c
View SolutionIf ABCDEF is a regular hexagon, them →AD+→EB+→FC equals 2→AB b. →0 c. 3→AB d. 4→AB
View Solution
