A particle is to move along the x−axis from x=0 to x=x1 while a conservative force, directed along the x−axis, acts on the particle. For each force defination presented in the figures the maximum magnitude of the force (F1) is the same for all cases. Rank the forces according to the change in potential energy associated with the motion shown. from most positive to most negative:
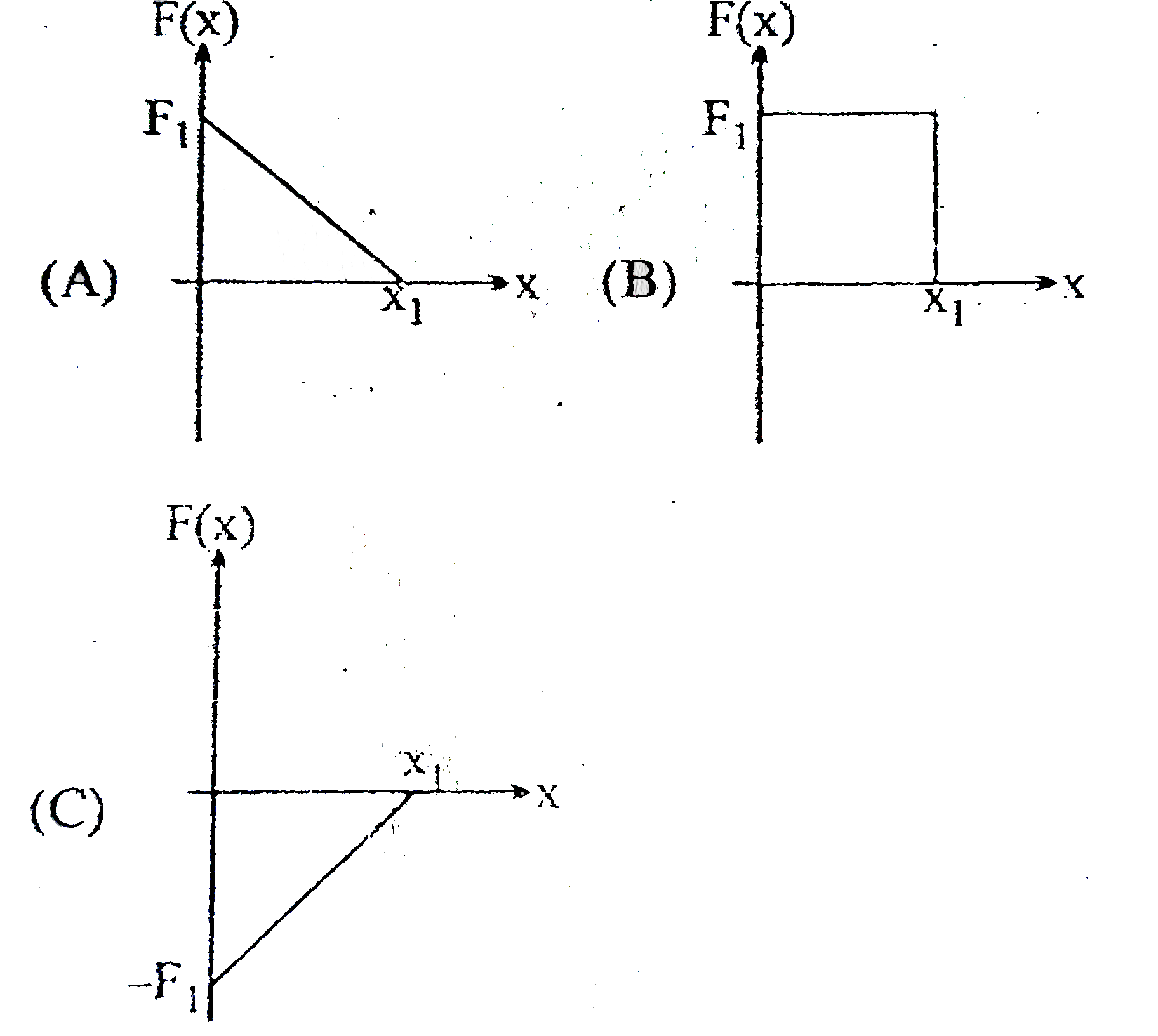 Solution in Gujrati
Solution in Gujrati
C,A,B
B,A,C
C,B,A
A,B,C
The correct Answer is:A
dU=−Fdx
⇒ΔU=−∫Fdx=− Area under the curve and x−axis
Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionThe force acting on a body moving along x-axis varies with the position of the particle shown in the figure. The body is in stable equilibrium at .
View SolutionTwo forces f1=4N and f2=3N are acting on a particle along positve X−axis and negative y−axis respectively. The resultant force on the particle will be−
View SolutionAs a particle moves along the x- axis, it is acted upon by a conservative force. The potential energy is shown below as a function of the coordinate x of the particle. Rank the labelled regions accoeording to the magnitude of force, least to greatest.
View SolutionA particle moving along the X-axis executes simple harmonic motion, then the force acting on it is given by
where, A and K are positive constants.
View SolutionThe given figure shows a plot of the time dependent force F_(x) acting on a particle in motion along the x-axis. What is the total impulse delivered by this force to the particle from time t = 0 to t = 2second?
View SolutionThe kinetic energy K of a particle moving along x axis varies with its position (x) as shown in the figure. The magnitude of force acting on particle at x = 9 m is -
View SolutionA conservative force acts on a particle as the particle moves along the positive x-axis from origin origin to x=2m . The force is parallel to x-axis. Now, consider four different cases, as shown in the figures, 1, 2, 3, and 4, where the forces is shown as a function of x. Rank the situations according to the change in potential energy associated with the force, least ( or most negative) to greatest ( or most positive).
View SolutionThe figure (A) and (B) shows two different arrangements of a spool being pulled with a constant force F in each case. Identify the direction of motion of centre of mass, and the direction of friction force in each case
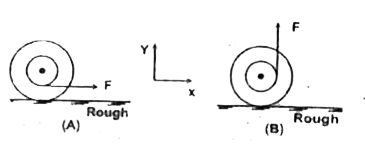
(i) The centre of mass moves along _______ x-axis in figure (A). (negative/positive)
(ii) The frictional force acts along ___________ x-axis in figure (A). (negative/positive)
(iii) The centre of mass moves along ____________ x-axis in figure (B). (negative/positive)
(iv) The frictional force acts along _____________ x-axis in figure (B). (negative/positive)
View SolutionThe kinetic energy K of a particle moving along x - axis varies its position (x) as shown in figure.

The magnitude of force acting on particle at x = 9m is
View SolutionThe kinetic energy K of a particle moving along x - axis varies with its position (x) as shown in figure The magnitude of force acting on particle at x = 9 mis
View SolutionA particle, moving along the x-axis, executes simple harmonic motion when the force acting on it is given by (A and k are positive constant.)………………
View SolutionThe force on a particle is directed along an x axis and given by F=F0(x/x0−1). Find the work done by the force in moving the particle from x=0 to x=2x0 by (a) plotting F(x) and measuring the work from the graph and (b) integrating F(x).
View Solution
