A particle moves on x-axis such that its KE varies as a relation KE=3t2 then the average kinetic energy of a particle in 0 to 2 sec is given by :Solution in Gujrati
6 joule
8 joule
4 joule
16 joule
The correct Answer is:A
Step by step video & image solution for A particle moves on x-axis such that its KE varies as a relation KE=3t^(2) then the average kinetic energy of a particle in 0 to 2 sec is given by : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- TEST PAPERBOOK - ALLEN CHAPTER - TEST PAPEREXERCISE - PHYSICS
4 Videos
- SIMPLE HARMONIC MOTIONBOOK - ALLEN CHAPTER - SIMPLE HARMONIC MOTIONEXERCISE - Example
1 Videos
- TEST PAPER 1BOOK - ALLEN CHAPTER - TEST PAPER 1EXERCISE - PHYSICS
11 Videos
Similar Questions
Choose the correct statement:
View SolutionChoose the correct statement:
View SolutionA rod with rectangular cross section oscillates about a horizontal axis passing through one of its ends and it behaves like a seconds pendulum, its length will be
View SolutionWhy are electric field lines perpendicular at a point on an equipotential surface of a conductor ?
View SolutionThe kinetic energy (KE) versus time graph for a particle moving along a straight line is as shown in the figure. The force versus time graph for the particle may be
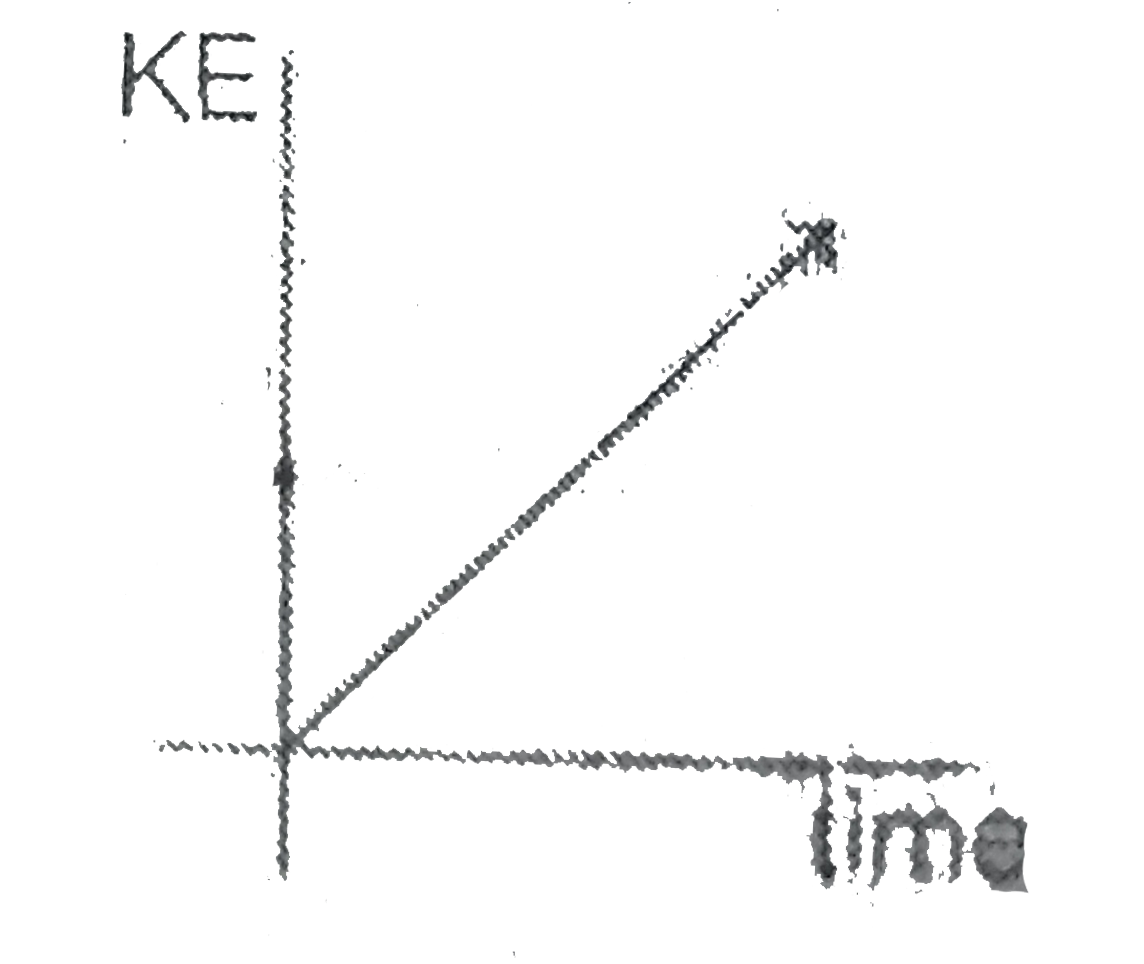
View SolutionThe kinetic energy of a particle of mass m moving with speed v is given by K=12mv2. If the kinetic energy of a particle moving along x-axis varies with x as K(x)=9−x2, then The region in which particle lies is :
View SolutionA particle is executing simple harmonic motion (SHM) of amplitude A, along the x-axis, about x = 0. When its potential Energy (PE) equals kinetic energy (KE), the position of the particle will be :
View SolutionAverage kinetic energy per molecule of a gas is related to its temperature as ¯¯¯¯KE=………………… .
View SolutionThe kinetic energy K of a particle moving along x - axis varies its position (x) as shown in figure.

The magnitude of force acting on particle at x = 9m is
View SolutionIf the particle is moving along a straight line given by the relation x=2−3t+4t3 where s is in cms., and t in sec. Its average velocity during the third sec is
View SolutionA particle is executing simple harmonic motion (SHM) of amplitude A, along the x-axis, about x = 0. When its potential Energy (PE) equals kinetic energy (KE), the position of the particle will be :
View SolutionIf the particle is moving along a straight line given by the relation x=2−3t+4t3 where s is in cms., and t in sec. Its average velocity during the third sec is
View SolutionFor a particle executing SHM. The kinetic energy 'K' is given by k=k0Cos2wt. the maximum value of KE is
View SolutionFor a particle executing SHM. The kinetic energy 'K' is given by k=k_(0) Cos^(2)wt. the maximum value of KE is
View SolutionFor a particle executing SHM. The kinetic energy 'K' is given by k=k0Cos2wt. The maximum value of KE is
View SolutionKinetic energy and momentum are related by the term KE is equal to _____.
View Solution
