A particle is projected from a point P with a velocity v at an angle θ with horizontal. At a certain point Q it moves at right angles to its initial direction. Then Solution in Gujrati
Velocity of particle at Q is vsinθ
Velocity of particle at Q is vcotθ
Time of flight from P to Q is (v/g)cosecθ
Time of flight from P to Q is (v/g)secθ
The correct Answer is:B, C
∵ Horizontal component of velocity remains constant
∴vsinθ=vcosθ (from figure) ∴v'=vcotθ
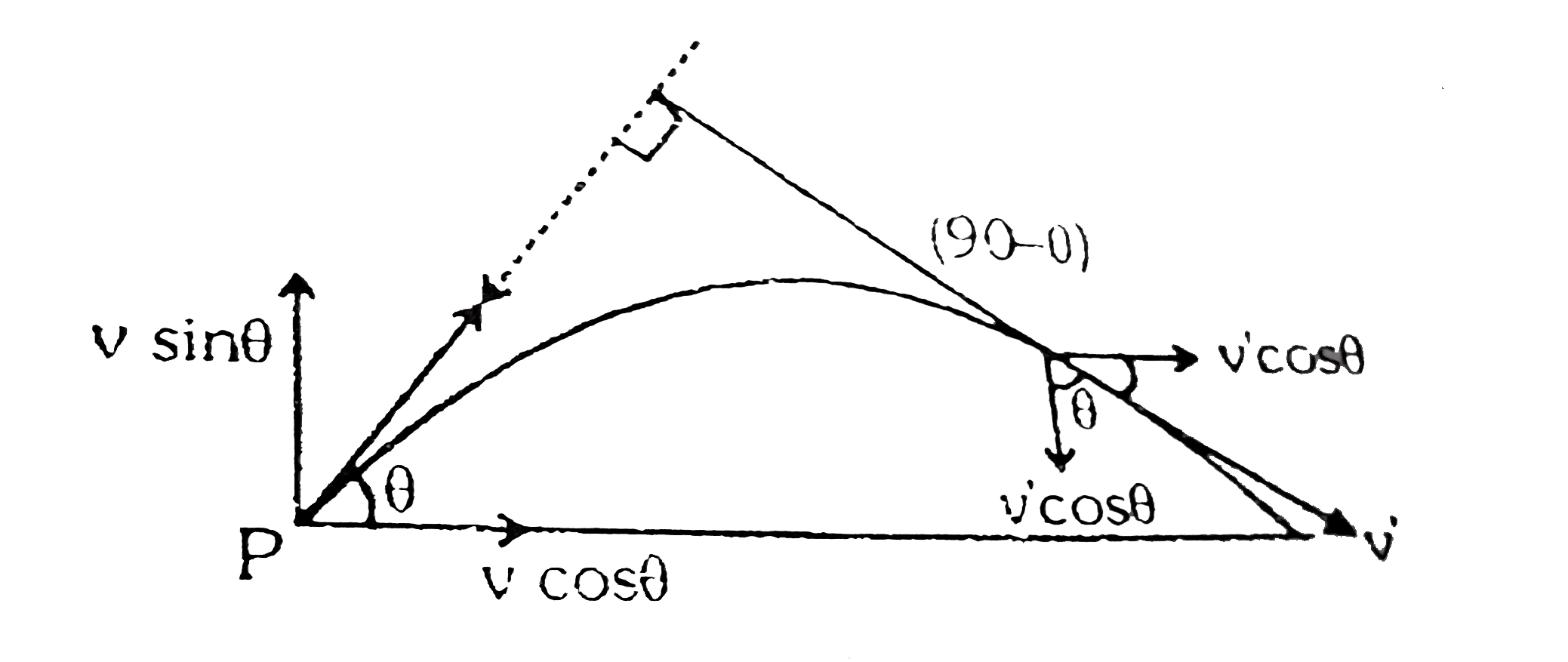
So from vy=uy+ayt→−v'cosθ
=sinθ−gt−vcos2θsinθ=vsinθ−gt∴t=vgcosecθ
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-03
6 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Assertion-Reason
20 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-01
55 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
The equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
View SolutionAssertion: A projectile is thrown with an initial velocity of (aˆi+bˆj)m/sec. If range of projectile is maximum then a=b.
Reason: In projectile motion, angle of projection is equal to 45∘ for maximum rang econdition.
View SolutionA bird moves from point (1,−2,3) to (4,2,3). If the speed of the bird id 10m/s, then the velocity of the bird is :-
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionA particle is projected from the ground with an initial speed of v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectroy is :
View SolutionA particle is projected with velocity v at an angle of θ with horizontal. The average angular velocity of the particle from the point of projection to impact equals:
View SolutionA particle is project d from point A with velocity u at an angle α with horizontal. In its parabolic path, at point P the particle is moving at right angles to its initial direction of projection. Its velocity at P is:
View SolutionA particle is projected from a point O with a velocity u at an angle α (upwards) to the horizontal. At a certain point P it moves at right angles to its initial direction. It follows that:
View SolutionA particle is projected from a point O with velocity u in a direction making an angle alpha upward with the horizontal. AT P , it is moving at right angles to its initial direction of projection . Its velocity at P is .
View SolutionA particle is projected from the ground with an initial speed of u at an angle of projection θ. The average velocity of the particle reaches highest point of trajectory is
View SolutionA particle is projected fro the ground with an initial speed v at an angle θ with horizontal. The average velocity of the particle between its point of projection and highest point trajectory is
View SolutionA particle is projected from the ground with an initial speed v at an angle theta with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is
View SolutionA particle is projected from the ground with an initial speed of v at a angle θ with horizontal. The average velocity of the particle between its point of projection and highest point of trajectory is
View SolutionA particle is projected from a point O with velocity u in a direction making an angle alpha upward with the horizontal. At P it is moving at right angle so its initial direction of projection. Its velocity at P is
View SolutionA particle is projected from the ground with an initial speed of v at an angle theta with horizontal . The average velocity of the particle between its point of projection and highest point of trajectory is :
View Solution
