Statement-I : If two particles, moving with constant velocities are to meet, the relative velocity must be along the line joining the two particles.
Statement-II : Relative velocity means motion of one particle as viewed from the other.Solution in Gujrati
Statement-I is true, Statement-II is true, Statement-II is correct explanation for Statement-I
Statement-I is true, Statement-II is true, Statement-II is NOT a correct explanation for Statement-I
Statement-I is true, Statement-II is false
Statement-I is false, Statement-II is true.
The correct Answer is:B
To meet, co-ordinates must be same. So in frame of one particle, second particle should approach it.
Topper's Solved these Questions
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#1
3 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - Comprehension#2
5 Videos
- KINEMATICSBOOK - ALLEN CHAPTER - KINEMATICSEXERCISE - EXERCISE-03
6 Videos
- ERROR AND MEASUREMENTBOOK - ALLEN CHAPTER - ERROR AND MEASUREMENTEXERCISE - Part-2(Exercise-2)(B)
22 Videos
- KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)BOOK - ALLEN CHAPTER - KINEMATICS (MOTION ALONG A STRAIGHT LINE AND MOTION IN A PLANE)EXERCISE - BEGINNER S BOX-7
8 Videos
Similar Questions
Distance is a scalar quantity. Displacement is a vector quqntity. The magnitude of displacement is always less than or equal to distance. For a moving body displacement can be zero but distance cannot be zero. Same concept is applicable regarding velocity and speed. Acceleration is the rate of change of velocity. If acceleration is constant, then equations of kinematics are applicable for one dimensional motion under the gravity in which air resistance is considered, then the value of acceleration depends on the density of medium. Each motion is measured with respect of frame of reference. Relative velocity may be greater/ smaller to the individual velocities.
A particle moves from A to B. Then the ratio of distance to displacement is :-
View SolutionA car is moving on a straight road. The velocity of the car varies with time as shown in the figure. Initially (at t=0), the car was at x=0, where, x is the position of the car at any time 't'.
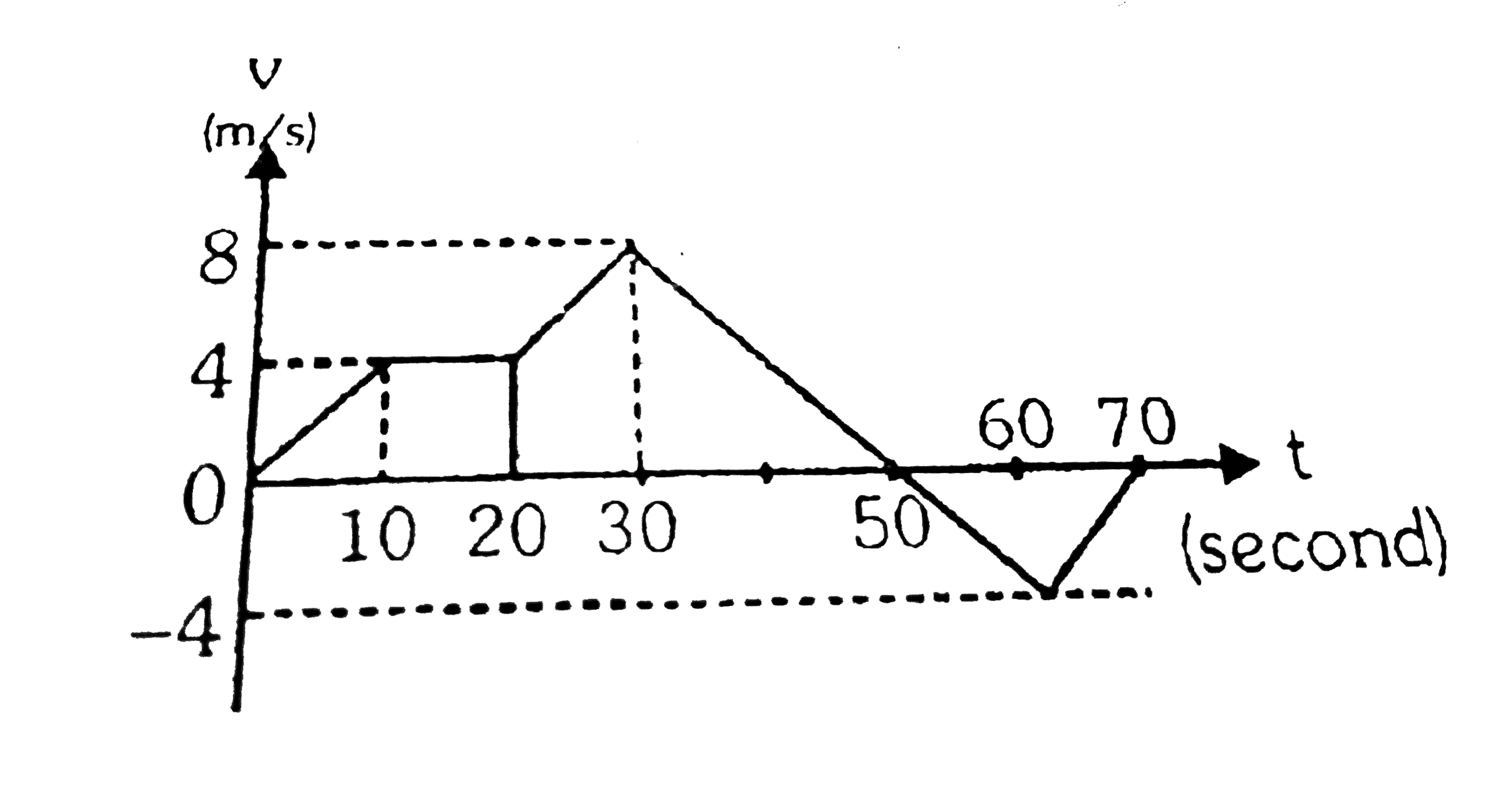
The variation of acceleration (a) with time (t) will be best represented by :-
View SolutionThe equation of one dimensional motion of the particle is described in column I. At t=0, particle is at origin and at rest. Match the column I with the statement in Column II.
Column IColumn II(A)x=(3t2+2)m(p)Velocity of particle at t=1s is 8m/s(B)v=8tm/s(q)Particle moves with uniform acceleration(C)a=16t(r)Particle moves with variable acceleration(D)v=6t−3t2(s)Particle will change its direction some time
View SolutionA cube has a side of length 1.2×10−2m. Calculate its volume.
View SolutionA football player kicks a ball at an angle of 30∘ with an initial speed of 20 m/s. Assuming that the ball travels in a vertical plane, calculate (a) the time at which the ball reaches the highest point (b) the maximum height reached (c) the horizontal range of the ball (d) the time for which the ball is in the air, (g=10m/s2)
View SolutionAssertion: If two particles, moving with constant velocities are to meet, the relative velocity must be along the line joining the two particles. Reason: Relative velocity means motion of one particle as viewed from the other.
View SolutionSTATEMENT-1: Two particles starts moving with velocities →V1&→V2 respectively in xy-plane. They can meet only if component of their velocity perpendicular to line joining them are equal.
STATEMENT-2: Realative velocity of a body w.r.t. other body is calculated along line joining two bodies.
View SolutionTwo particles move toward each other with velocities v_1=0.50c and v_2=0.75c relative to a laboratory frame of reference. Find: (a) the approach velocity of the particles in the laboratory frame of reference, (b) their relative velocity.
View SolutionTwo relativistic particles move at right angles to each other in a laboratory frame of reference, one with the velocity v_1 and the other with the velocity v_2 . Find their relative velocity.
View SolutionTwo particles start simultaneously from the same point and move along two straight lines. One with uniform velocity v and other with a uniform acceleration a. if alpha is the angle between the lines of motion of two particles then the least value of relative velocity will be at time given by
View SolutionTwo particles start from rest simultaneously and are equally accelerated throughout the motion, the relative velocity ofone with respect to other is :
View SolutionShown in the figure are the velocity time graphs of the two particle P1 and P2 moving in same straight line in same direction. Which of the following statements about their relative motion is true?
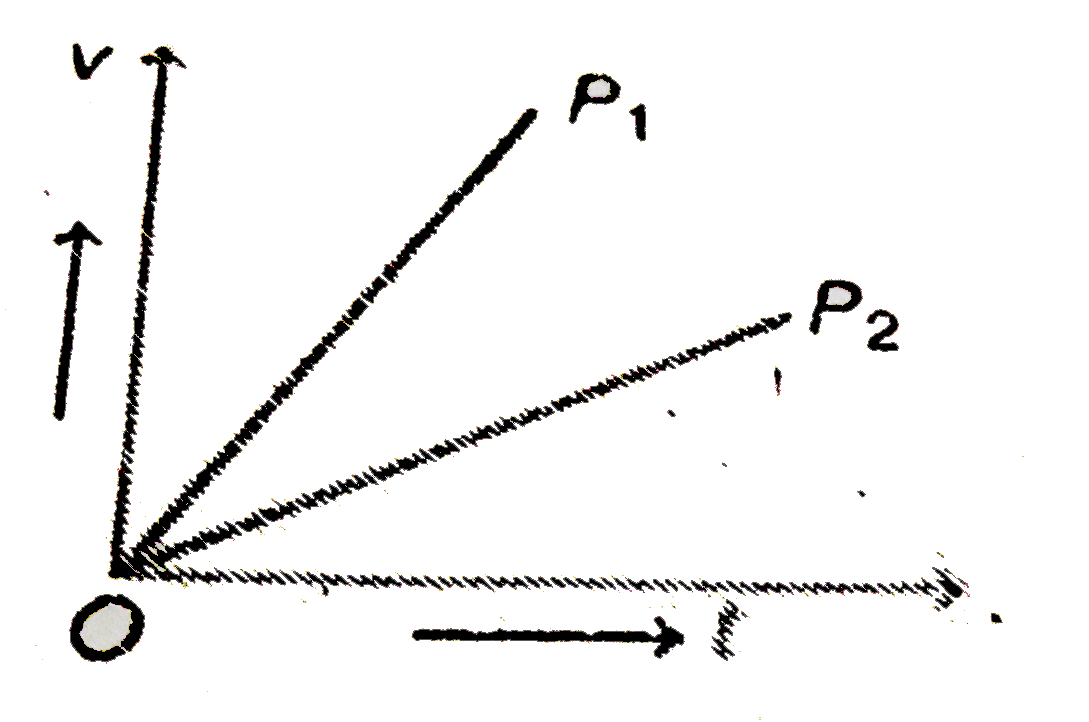
Their relative velocity
View SolutionTwo particles are moving with velocities v_(1) and v_2 . Their relative velocity is the maximum, when the angle between their velocities is
View SolutionShown in the figure are the velocity time graphs of the two particles P_1 and P_2 . Which of the following statements about their relative motion is true ? Theire relative velocity
View SolutionStatement I : Acceleration of a moving particle can change its direction without any change in the direction of velocity.
Statement II : If the direction two particles moving with constant velocities always remains vector also changes.
View SolutionStatement I : Distance between two particles moving with constant velocities always remains constant.
Statement II : The relative motion between two particles moving with constant velocities always remains constant.
View Solution
